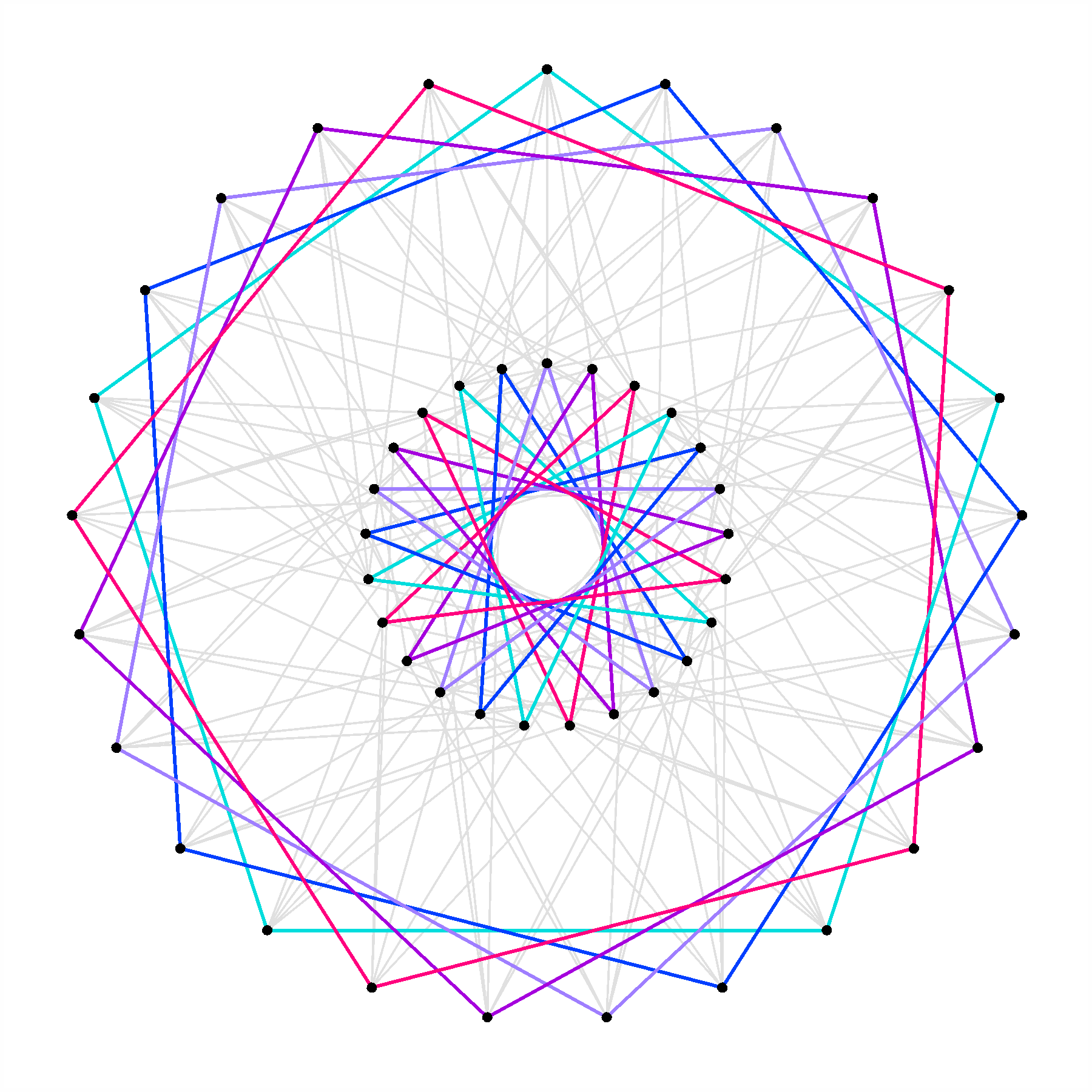
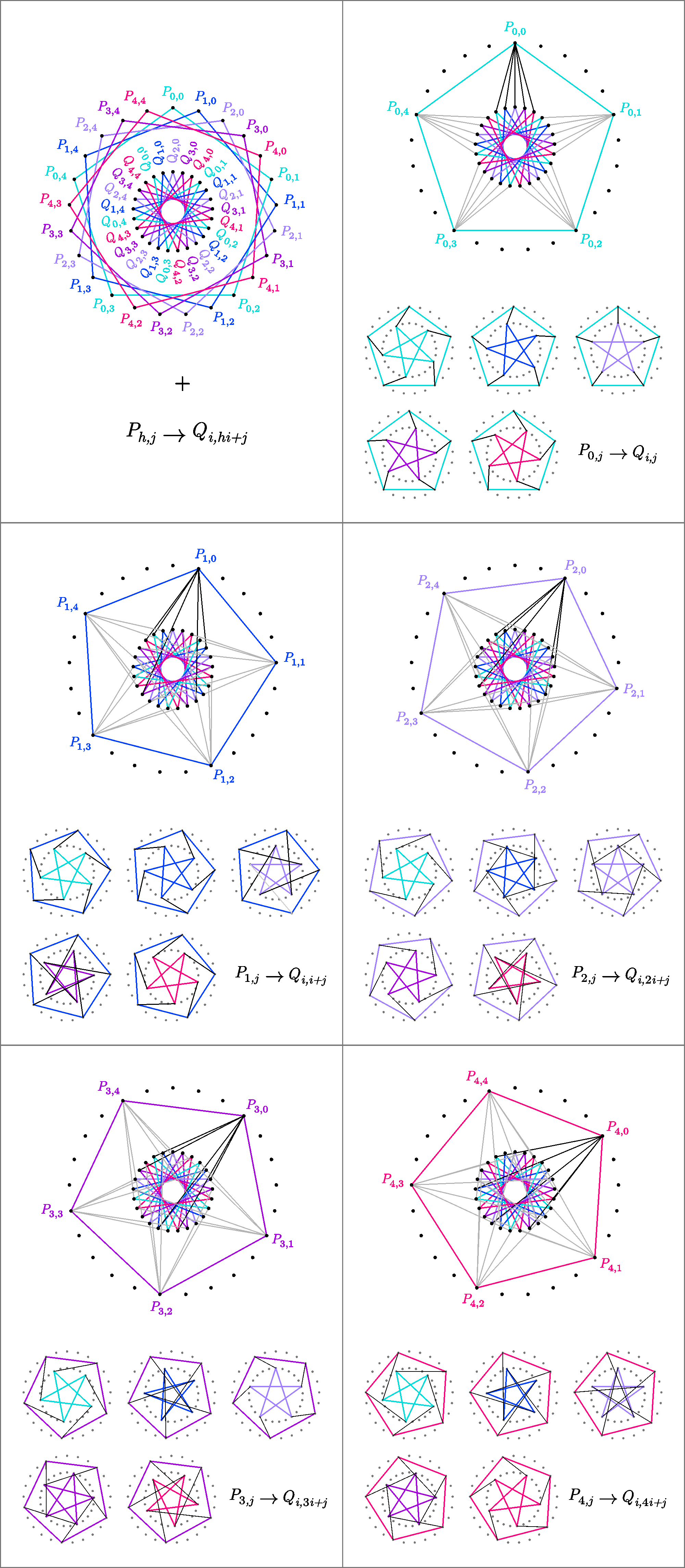
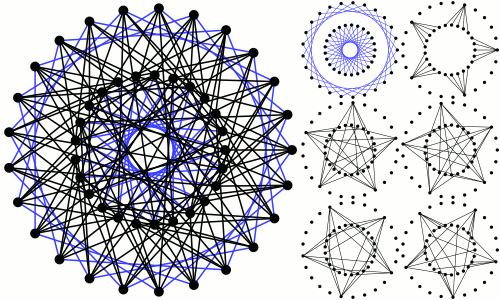
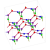
This is the Hoffman–Singleton graph, a remarkably symmetrical graph with 50 vertices and 175 edges. There is a beautiful way to construct the Hoffman–Singleton graph by connecting 5 pentagons to 5 pentagrams.

In what follows, all indices lie in \(\mathbb{Z}/5\): that is, the integers mod 5.

Take five pentagons \(P_h\): graphs with 5 vertices such that vertex \(j\) is adjacent to vertices \(j-1\) and \(j+1\). Take 5 pentagrams \(Q_i\): graphs with 5 vertices such that vertex \(j\) is adjacent to vertices \(j-2\) and \(j+2\). Now join each vertex \(j\) of pentagon \(P_h\) to the vertex \(hi+j\) of pentagram \(Q_i\). The result is the Hoffman–Singleton graph.

Félix de la Fuente constructed the above picture of the Hoffman–Singleton graph using this method. He explains the details here:

In this diagram \(P_{h,j}\) is the \(j\)th vertex of the pentagon \(P_h\), while \(Q_{i,k}\) is the \(k\)th vertex of the pentagram \(Q_i\). Each vertex \(P_{h,j}\) is connected to 5 vertices \(Q_{hi+j}\). Félix de la Fuente shows how this connects each pentagon to all 5 pentagrams, forming 5 copies of the ‘Petersen graph’. For more on the Petersen graph, see this earlier post:

• Petersen graph.

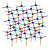
Here is another image of the same construction:

The Hoffman–Singleton graph has 252,000 symmetries. Not surprisingly, they’re deeply connected to the math you can do with the numbers 5 and 25. They form a group isomorphic to the group called \(\mathrm{P}\Sigma \mathrm{U}(3,\mathbb{F}_{25})\).

To understand this group, note that \(\mathbb{F}_{25}\), the field with 25 elements, can be obtained from \(\mathbb{F}_5\), the field with 5 elements, by adjoining a square root \(i\) of some element that does not have a square root in \(\mathbb{F}_5\). This element will then have 2 distinct roots in \(\mathbb{F}_{25}\), namely \(i\) and \(-i\), and there is an automorphism of \(\mathbb{F}_{25}\) that exchanges them, called the Frobenius automorphism. This automorphism also sends each element of \(\mathbb{F}_{25}\) to its 5th power.

Since it switches \(i\) and \(-i\), the Frobenius automorphism of \(\mathbb{F}_{25}\) is similar to complex conjugation. We can use it to define unitary matrices over \(\mathbb{F}_{25}\), and thus the unitary group \(\mathrm{U}(3,\mathbb{F}_{25})\) consisting of \(3 \times 3\) unitary matrices, and its subgroup \(\mathrm{SU}(3,\mathbb{F}_{25})\), the special unitary group, consisting of those with determinant 1.

If we take \(\mathrm{SU}(3,\mathbb{F}_{25})\) and mod out by its center, consisting of matrices that are multiples of the identity, we obtain the projective special unitary group \(\mathrm{PSU}(3,\mathbb{F}_{25})\). The 2-element group generated by the Frobenius automorphism acts on \(\mathrm{PSU}(3,\mathbb{F}_{25})\). Thus, we can form the semidirect product of \(\mathbb{Z}/2\) and \(\mathrm{PSU}(3,\mathbb{F}_{25})\), obtaining a group called \(\mathrm{P}\Sigma \mathrm{U}(3,\mathbb{F}_{25})\).

Puzzle 1: Show that \(\mathrm{P}\Sigma \mathrm{U}(3,\mathbb{F}_{25})\) has 252,000 elements.

Puzzle 2: Can you use the description of the Hoffman–Singleton graph in terms of pentagons and pentagrams to prove that its symmetry group contains \(\mathrm{P}\Sigma \mathrm{U}(3,\mathbb{F}_{25})\)?

The symmetry group of the Hoffman–Singleton graph acts transitively on the ‘flags’, where a flag is a pair consisting of a vertex and an edge incident to that vertex. The Hoffman–Singleton graph is thus called a symmetric graph.

The stabilizer of a vertex of the Hoffman–Singleton graph is isomorphic to the symmetric group on 7 letters, \(\mathrm{S}_7\). The stabilizer of an edge is isomorphic to \(\mathrm{Aut}(\mathrm{A}_6)\), where \(\mathrm{A}_6\) is the alternating group on 6 letters. (The group \(\mathrm{Aut}(\mathrm{A}_6)\) has four times as many elements as \(\mathrm{A}_6\).) Both these stabilizers are maximal subgroups of the symmetry group of the Hoffman–Singleton graph.

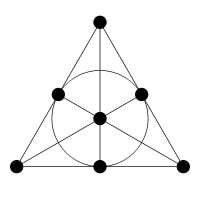
There is also a more subtle way to construct the Hoffman–Singleton graph starting from the Fano plane: the projective plane over the field with 2 elements.

The Fano plane has 7 points and 7 lines, with 3 points on each line and 3 lines through each point:

The symmetry group of the Fano plane has 168 elements. So, the number of different Fano plane structures on a 7-element set is

$$ 7! / 168 = 30 $$

Call each of these a Fano.

Fix a 7-element set \(S\). This set has

$$ {7 \choose 3} = 35 $$

3-element subsets, which we will call triads. Choose a triad \(L \subset S\). Since there are \(30\) Fanos, each with 7 lines, and just 35 triads, there are

$$ \frac{30 \cdot 7}{35} = 6 $$

Fanos for which \(L\) is a line.

Puzzle 3. Show that for any Fano \(F\), there are 14 other Fanos \(F’ \ne F\) that have a line in common with \(F\). (That is, some triad is a line in both \(F\) and \(F’\).)

Now, fix a Fano and consider all 15 Fanos that have a line in common with \(F\).

To build the Hoffman–Singleton graph, take these 15 Fanos and all 35-element subsets of \(S\) as vertices. Draw an edge between any triad and any Fano that has it as a line. Draw an edge between any two 3-element subsets that are disjoint. Never draw an edge between two Fanos.

The resulting graph is the Hoffman–Singleton graph! It has the 50 vertices corresponding to the 35 triads and 15 Fanos. Each vertex has degree 7. A vertex corresponding to a Fano is connected to 7 triads, since the Fano plane has 7 lines. Each triad is connected to the 3 Fanos that include it and the 4 triads it is disjoint from.

Puzzle 3. Why can the Hoffman–Singleton graph be built this way? Being built from 5 pentagons and 5 pentagrams, it’s not surprising that its symmetry group is connected to the number 5 and the field \(\mathbb{F}_{25}\). But the Fano plane seems unrelated to this.

My best guess about Puzzle 3 is that it’s connected to the stabilizer of any vertex of the Hoffman–Singleton graph being \(\mathrm{S}_7\). This group can act on a 7-point set, and thus on the set of Fanos.

The Hoffman–Singleton graph is a (7,5)-cage, meaning a graph where each vertex has exactly 7 neighbors, the shortest cycles have length 5, and it has as few vertices as possible while possessing both these properties. This follows from the fact that the Hoffman–Singleton graph is a Moore graph. In fact, it is the largest known Moore graph, apart from complete graphs, and it arose in Hoffman and Singleton’s attempt to classify Moore graphs:

• Alan J. Hoffman and Robert R. Singleton, Moore graphs with diameter 2 and 3, IBM Journal of Research and Development 5 (1960), 497–504.

The Hoffman–Singleton theorem states that in a Moore graph with girth 5, every vertex must have 2, 3, 7, or 57 neighbors. The existence of one where every vertex has 57 neighbors is unknown.

For more, see:

• Hoffman–Singleton graph, Wikipedia.

• Andries E. Brouwer, Hoffman–Singleton graph.

• Asif Zaman, Moore graphs with diameter 2 and 3.

The ‘pentagons and pentagrams construction’ of the Hoffman–Singleton graph was first given by Robertson, but it was used to study the graph’s symmetries here:

• P. R. Hafner, The Hoffman–Singleton graph and its automorphisms, Journal of Algebraic Combinatorics 18 (2003), 7–12.

If you get stuck on Puzzle 2, this paper holds useful clues. They also show that the Hoffman–Singleton graph contains exactly 1260 cycles of length 5. I do not know the answer to this question:

Puzzle 4: Does the symmetry group of the Hoffman–Singleton graph act transitively on the set of cycles of length 5?

An affirmative answer would explain why the order of the symmetry group is divisible by the number of 5-cycles:

\[ \frac{252,000}{1260} = 200 . \]

Spoiler

Here is an answer to Puzzle 3, provided by Greg Egan. However, there may be more intuitive ways to count the Fanos that share a line with a given Fano.

For the Fano:

{{1,2,4},{1,3,7},{1,5,6},{2,3,5},{2,6,7},{3,4,6},{4,5,7}}

the 14 other Fanos that share exactly one line with it come in pairs where the common line is each of the 7 lines in the original Fano:

{{1,2,4},{1,3,5},{1,6,7},{2,3,6},{2,5,7},{3,4,7},{4,5,6}}
{{1,2,4},{1,3,6},{1,5,7},{2,3,7},{2,5,6},{3,4,5},{4,6,7}}

{{1,2,5},{1,3,7},{1,4,6},{2,3,6},{2,4,7},{3,4,5},{5,6,7}}
{{1,2,6},{1,3,7},{1,4,5},{2,3,4},{2,5,7},{3,5,6},{4,6,7}}

{{1,2,3},{1,4,7},{1,5,6},{2,4,6},{2,5,7},{3,4,5},{3,6,7}}
{{1,2,7},{1,3,4},{1,5,6},{2,3,6},{2,4,5},{3,5,7},{4,6,7}}

{{1,2,6},{1,3,4},{1,5,7},{2,3,5},{2,4,7},{3,6,7},{4,5,6}}
{{1,2,7},{1,3,6},{1,4,5},{2,3,5},{2,4,6},{3,4,7},{5,6,7}}

{{1,2,3},{1,4,6},{1,5,7},{2,4,5},{2,6,7},{3,4,7},{3,5,6}}
{{1,2,5},{1,3,6},{1,4,7},{2,3,4},{2,6,7},{3,5,7},{4,5,6}}

{{1,2,3},{1,4,5},{1,6,7},{2,4,7},{2,5,6},{3,4,6},{3,5,7}}
{{1,2,6},{1,3,5},{1,4,7},{2,3,7},{2,4,5},{3,4,6},{5,6,7}}

{{1,2,5},{1,3,4},{1,6,7},{2,3,7},{2,4,6},{3,5,6},{4,5,7}}
{{1,2,7},{1,3,5},{1,4,6},{2,3,4},{2,5,6},{3,6,7},{4,5,7}}

The picture of the pentagons and pentagrams construction was created by Claudio Rocchini and placed on Wikicommons under a GNU Free Documentation license.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!