The Cairo tiling is a tiling of the plane by pentagons.
To construct the Cairo tiling, we can start with a snub square tiling:
The snub square tiling is a uniform tiling of the plane by squares and equilateral triangles, with 2 squares and 3 triangles meeting at each vertex, arranged in the pattern 3.3.4.3.4.
Starting from the snub square tiling, form the dual tiling. This has a vertex at the center of each square or triangle, with one edge crossing each edge of the snub square tiling:
The result is the Cairo tiling!
This tiling gets its name because it is apparently used to tile some streets in Cairo.
Puzzle 1. Is this really true? Which streets? Has someone taken a photograph?
Puzzle 2. What are the internal angles and side lengths of the pentagons in the Cairo tiling?
Carbon can form flat molecular sheets consisting of regular hexagons, called graphene. In February 2015, this article argued that carbon could also form sheets in which the atoms lay at the vertices of a Cairo tiling:
• Shunhong Zhang, Jian Zhou, Qian Wanga, Xiaoshuang Chen, Yoshiyuki Kawazoe and Puru Jena, Penta-graphene: a new carbon allotrope, Proceedings of the National Academy of Sciences 112 (2015), 2372–2377.
The authors did calculations to show that this hypothetical material would be stable. However, more recently a paper has come out arguing for the opposite conclusion:
• Christopher P. Ewels, Xavier Rocquefelte, Harold W. Kroto, Mark J. Rayson, Patrick R. Briddon, and Malcolm I. Heggie, Predicting experimentally stable allotropes: instability of penta-graphene, Proceedings of the National Academy of Sciences 112 (2015), 15609–15612.
This paper has beautiful pictures showing how penta-graphene could transform into ordinary graphene. You can read a summary of the dispute here:
• Heather Zeiger, Criteria to predict experimentally stable allotropes, Phys.org, 5 January 2016.
The above picture of the Cairo tiling was made by Tom Ruen and placed it on Wikicommons with a Creative Commons Attribution-Share Alike 4.0 International license. Tom Ruen also created the picture of the snub square tiling and placed it on Wikicommons with the same license. The picture of the square snub tiling together with its dual was made by a German Wikicommons user going by the name of TED-43, and he placed it on Wikicommons with a GNU Free Documentation License, version 1.2.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!



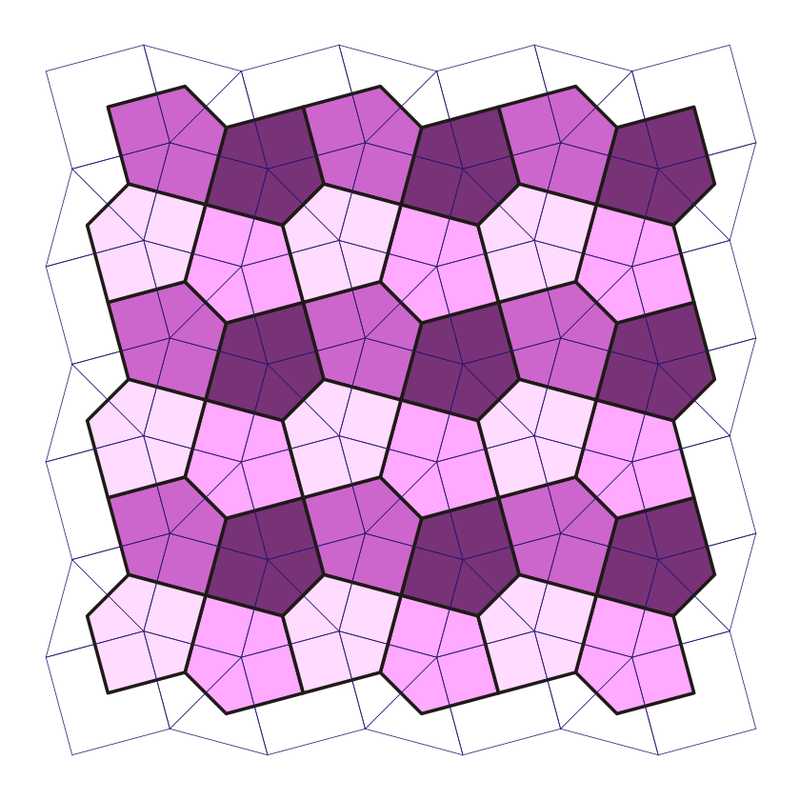



Cool, I’ve admired the Cairo tiling before, but I had no idea you can get it by dualizing the snub square tiling. I really like TED-32’s picture! It has the solution to puzzle 2.
I can’t answer puzzle 1, because I’ve forgotten where I read about it, but as far as I remember the reason is just that it’s rather common there, often found on facades.
I couldn’t find pictures of actual Cairo Tiling in Cairo but I did find Lego compatible Cairo Tiles!
https://www.thingiverse.com/thing:1263736
(Well, you have to print them first.)
I live in Cairo, there are plenty. and I found this blog post http://www.tess-elation.co.uk/cairo-tiling mentioning some of the places where you can find them.
Nice, but when you say that the snub cube tiling comes in two mirror-image forms, that’s only true for a different coloring than the one you show, which is actually mirror symmetric. The snub hexagonal tiling also has this property. https://en.wikipedia.org/w/index.php?title=Snub_hexagonal_tiling
Thanks, I’ll fix that. I was meaning to talk about the tiling itself, not any particular coloring. And as you note, this is mirror-symmetric. My eyes fooled me: starting from any square the neighboring and next-neighboring triangles form a pattern with a handedness… but both kinds of handedness appear, depending on which square you start with.
Also the snub cube is enantiomorphic, so you would think the snub square tiling would be!
“The result is the Cairo tiling. Like the snub square tiling, it comes in two mirror-image forms.”
Should this line be edited also? AFAICT, there are no mirror image forms to the Cairo tiling either.
Yes, thanks. I fixed it.
The snub square tiling and its dual illustrate the duality between the Voronoi diagram and the Delaunay triangulation associated to the same set of points. I generated Voronoi and Delaunay here https://plot.ly/~empet/13511/voronoi-delaunay-duality/ and the only difference is that a diagonal edge in each square of the snub tiling is missing.
The way these images are tilted, the symmetry and lack of handed-ness is less obvious.
A more intuitive tilt is to embed the tiling within a square tiling – such that each square is occupied by a >-< tree. (The minimal length network to join all four corners.)
So, to solve puzzle #2 using my Steiner Tree observation, each square of the virtual tiling contains 5 line segments. The ones leading to the four corners are longer, with a shorter segment in the center (Steiner Tree on four corners of a square). They meet at angles of 120 degrees, giving us the angles of the places where three segments meet. By more obvious symmetry, the other places have angles of 90 degrees (where four segments meet).
What about the segment lengths? Well, let’s call the longer segments length 1. This means the virtual square grid edge is sqrt(3) in length. The shorter line segments are thus of length sqrt(3) – 1/2 – 1/2 = sqrt(3)-1.
To further expand on my Steiner Tree thoughts…the tessellation doesn’t need to be constructed using minimal Steiner Trees. In fact, you can adjust the angles such that the pentagon edges all have the same length. Two non-neighboring internal angles must be 90 degrees, but the other angles need not be 120 degrees. I’m not sure what the angles are in the case when all edges are of the same length.
Puzzle 1: http://www.tess-elation.co.uk/cairo-tiling
Yes, this is the royal answer to Puzzle 1! There’s a lot of material on the Cairo tiling on this page:
• David Bailey’s World of Escher-like Tessellations, Cairo tiling.
If you look at left on this page, you’ll find lots of links to other pages, including:
• Pictures of sightings 1: sightings in Cairo and surrounding districts.
• Pictures of sightings 2: sightings outside Cairo, but still in Egypt.
Bailey is admirably obsessive about this!
That mistake, that the snub square tiling should have chirality, is a prominent one. Regrettably I can’t find the reference just now, or remember who it was. However, the illusion goes away if you align a triangle-triangle edge with the horizon.
Hi: thx for pictures in mathematics I am a teachear in. Iran and I. Use them for my classes ???????????