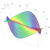
This is the free modular lattice on 3 generators, as drawn by Jesse McKeown. First discovered by Dedekind in 1900, this structure turns out to have an interesting connection to 8-dimensional Euclidean space.
The set of subspaces of any vector space \(V\) is a lattice: that is, a partially ordered set where every finite subset has a greatest lower bound and a least upper bound.
The ordering is defined by saying \(A \le B\) when the subspace \(A\) is contained in the subspace \(B\). The greatest lower bound of \(A \) and \(B\), denoted \(A \wedge B\), is just the intersection \(A \cap B\), while the least upper bound of \(A\) and \(B\), denoted \(A \vee B\), is the smallest subspace containing \(A \cup B\). The greatest lower bound of the empty set, or top element \(\top\), is the whole space \(V\), while the least upper bound of the empty set, or bottom element \(\bot\), is the subspace \(\{0\}\).
A lattice is distributive if
$$ A \vee (B \wedge C) = (A \vee B) \wedge (A \vee C) $$
holds for all \(A,B,C\). (Surprisingly, this is equivalent to requiring the law with the roles of \(\vee\) and \(\wedge\) reversed.) The lattice of subspaces of a finite-dimensional vector space is not distributive, but it’s always modular, meaning that the distributive law holds when \(A \le B\) or \(A \le C\).
The concept of a lattice can also be defined in a purely algebraic way. Namely, we can define a lattice to be a set with binary operations \( \vee \) and \(\wedge \) that are commutative, associative, and obey the absorption laws:
$$ A \wedge (A \vee B) = A , \qquad A \vee (A \wedge B) = A $$
together with elements \(\bot\) and \(\top\) that serve as identities for \(\vee\) and \(\wedge\), respectively. Starting from this we may define \(A \le B\) to mean \(A = A \wedge B\), or equivalently \(B = A \vee B\).
Since a lattice and also a modular lattice is a purely algebraic structure, ideas from universal algebra allow us to define the free modular lattice on any number of generators. This is roughly one where every element is built from the generators using \(\vee, \wedge, \top\) and \(\bot\) and no relations hold except those that follow from the definition of modular lattice.
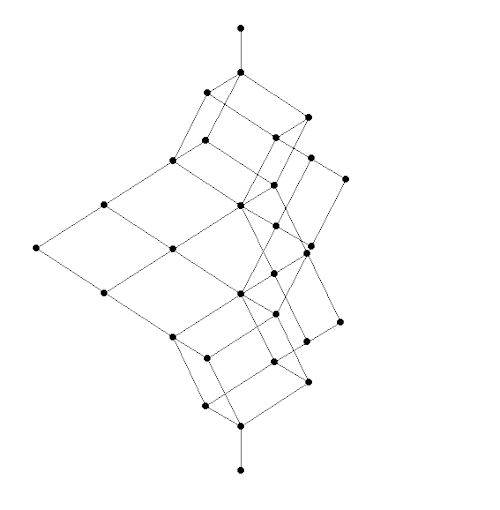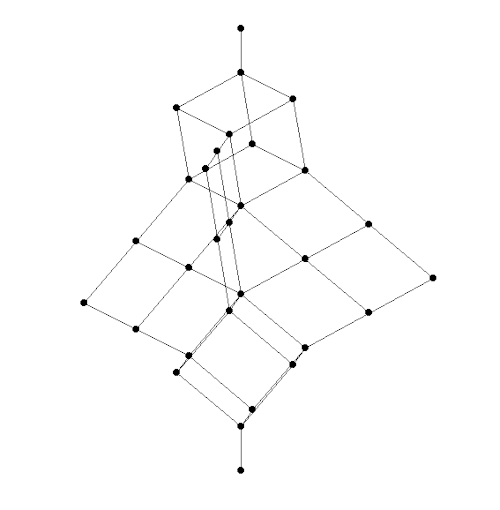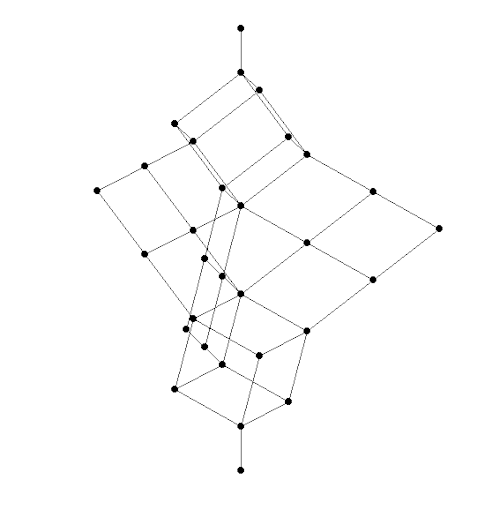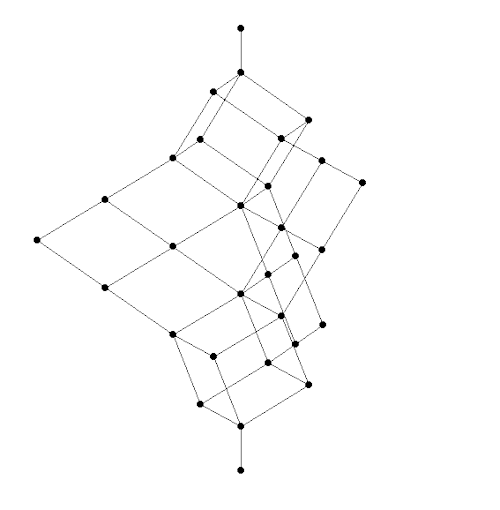
A remarkable fact, discovered by Dedekind in 1900, is that the free modular lattice on 3 generators has 30 elements, while the free modular lattice on 4 or more generators is infinite. The Hasse diagram of the free modular lattice on 3 generators is shown above. This has one dot for each lattice element, and \(A \le B\) iff we can go from the dot for \(A\) to the dot for \(B\) by climbing upwards along edges.
Here we are simplifying the actual history. In fact, Dedekind worked with a definition of lattice, still widely used, that does not require the existence of \(\bot\) and \(\top\). Thus, his free modular lattice on 3 generators had only 28 elements: it was missing the bottom and top dots in the picture above. It still had a bottom and top element, but these were not ‘free’: they could be defined in terms of the generators.
If we call the 3 generators \(X,Y,\) and \(Z\), Dedekind’s 28-element lattice looks like this:
Notice that this picture has 9 levels, or ‘ranks’. The generators \(X,Y,Z\) are on the middle rank. The top 3 ranks form a cube: this consists of \(X \vee Y\), \(X \vee Z\), \(Y \vee Z\) and all elements formed from these using \(\wedge\) and \(\vee\). Dually, the bottom 3 ranks form a cube consisting of \(X \wedge Y\), \(X \wedge Z\), \(Y \wedge Z\) and the elements formed from these via \(\wedge\) and \(\vee\).
Dedekind showed that his 28-element lattice could be represented as subspaces of an 8-dimensional vector space. To do this, he chose three subspaces \(X,Y,Z \subseteq \mathbb{R}^8\) and showed that the lattice they generate has 28 elements.
It’s not a coincidence that 8-dimensional space shows up in this problem! Let us see why.
Start with the Dynkin diagram of \(\mathfrak{so}(8)\), which is the Lie algebra of \(\mathrm{SO}(8)\), the group of rotations in 8 dimensions:
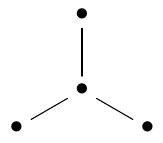
If we draw arrows on its edges like this:
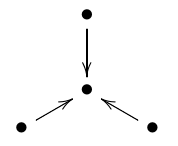
we get a directed graph, also known as a quiver. Let us call this particular directed graph the D4 quiver, after the name of the Dynkin diagram.
This quiver is closely connected to a famous puzzle: the 3 subspace problem. This problem asks us to classify triples of subspaces of a finite-dimensional vector space \(L\), up to invertible linear transformations of \(L\). It turns out that for any choice of the dimension of \(L\) there are finitely many possibilities. This is surprisingly nice compared to the 4 subspace problem, where there are infinitely many possibilities.
One way to solve the 3 subspace problem is to note that 3 subspaces \(L_1,L_2,L_3 \subseteq L\) give a representation of the \(\mathrm{D}_4\) quiver. This fact is trivial: by definition, a representation of the \(\mathrm{D}_4\) quiver is just a triple of linear maps like this:
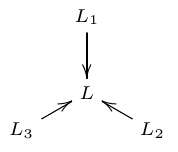
and here we are taking those to be inclusions. The nontrivial part is how we can use this viewpoint, together with some quiver representation theory, to solve the 3 subspace problem.
There is an obvious notion of two representations of the \(\mathrm{D}_4\) quiver being isomorphic. We can also take direct sums of quiver representations. We define an indecomposable representation to be one that it is not a direct sum of two others unless one of those others is trivial.
It is a remarkable fact, a spinoff of Gabriel’s theorem, that indecomposable representations of any quiver coming from a Dynkin diagram correspond in a natural one-to-one way with positive roots of the corresponding Lie algebra. As mentioned, the Lie algebra corresponding \(\textrm{D}_4\) is \(\mathfrak{so}(8)\), the Lie algebra of the group of rotations in 8 dimensions. This Lie algebra has 12 positive roots. So, the \(\textrm{D}_4\) quiver has 12 indecomposable representations which we list below. The representation coming from any triple of subspaces \(X, Y, Z \subseteq V\) must be a direct sum of these indecomposable representations, so we can classify the possibilities and solve the 3 subspace problem.
What does this have to do with the free modular lattice on 3 generators?
Given any representation \(f_i : L_i \to L\) of the \(\mathrm{D}_4\) quiver, the images of the maps \(f_i\) generate a sublattice \(\mathcal{L}\) of the lattice of all subspaces of \(L\). \(\mathcal{L}\) is a modular lattice with 3 generators. So, representations of the \(\mathrm{D}_4\) quiver give modular lattices with 3 generators. Moreover we have:
Theorem 1. If we take a direct sum of indecomposable representations of the \(D_4\) quiver, one from each isomorphism class, we obtain a representation of the \(D_4\) quiver whose corresponding modular lattice is the free modular lattice on 3 generators. In this representation, say \(f_i : L_i \to L\), the spaces \(\mathrm{im} (f_i)\) have dimension 5 and the space \(L\) has dimension 10. 10 is the smallest possible dimension for a vector space containing subspaces that generate a copy of the free modular lattice on 3 generators.
Proof. This will follow from Theorem 2 below. ▮
Let us call a representation of the \(\mathrm{D}_4\) quiver injective if all 3 maps \(f_i : L_i \to L\) are injective. Of the indecomposable representations of the \(\mathrm{D}_4\) quiver, exactly 3 are not injective:
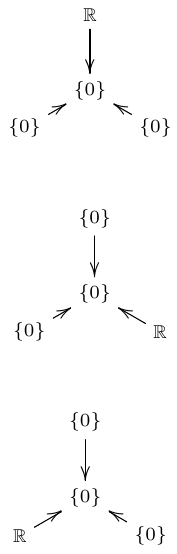
Note that these representations contribute trivially to the direct sum in Theorem 1. So, we can leave them out of this direct sum without affecting the result. This reduces Theorem 1 to
Theorem 2. If we take a direct sum of injective indecomposable representations of the \(D_4\) quiver, one from each isomorphism class, we obtain an injective representation of the \(D_4\) quiver whose corresponding modular lattice is the free modular lattice on 3 generators. In this representation, say \(f_i : L_i \to L\), the spaces \(L_i\) have dimension 5 while \(L\) has dimension 10. 10 is the smallest possible dimension for a vector space containing subspaces that generate a copy of the free modular lattice on 3 generators.
Proof. – It is clear that the direct sum of injective representations is injective. The rest will follow from Theorem 3. ▮
If we want to get Dedekind’s 28-element lattice, we need to leave out two injective indecomposable representations from the direct sum. To understand what is special about these two, and explicitly construct Dedekind’s lattice, let us go ahead and list the 12 indecomposable representations of the \(\mathrm{D}_4\) quiver.
For the 9 injective ones, we can assume without loss of generality that the maps are inclusions of subspaces. One of the injective indecomposable representations involves a triple of subspaces of zero dimension, while another involves a triple of subspaces that all equal the space they are included in:
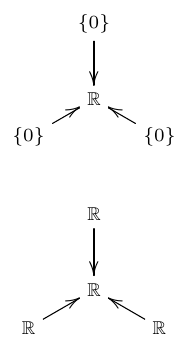
The remaining 7 injective indecomposable representations are the ones relevant to Dedekind’s 28-element lattice. We call them \(A, B, C, D, E, F\) and \(G\):
\(A\):
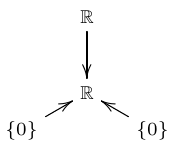
\(B\):
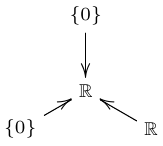
\(C\):
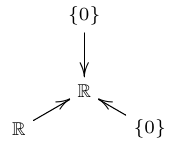
\(D\):
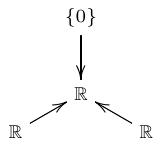
\(E\):
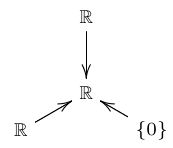
\(F\):
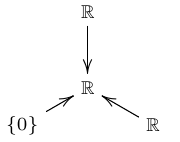
\(G\):
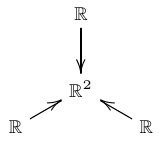
If we take the direct sum of all 7 of these quiver representations we obtain a representation that we call
Here the central dot of the \(D_4\) quiver has been assigned a vector space \(V\) which contains 3 subspaces \(X,Y,Z\). We have:
Theorem 3. The modular lattice generated by \(X,Y,Z \subset V\) is the free modular lattice on 3 generators with its top and bottom removed: that is, Dedekind’s 28-element lattice. \(V\) is 8-dimensional, and Dedekind’s lattice cannot be embedded in the lattice of subspaces of a vector space of dimension \(\lt 8\).
Theorem 3 easily implies Theorem 2. To prove Theorem 2, we shall explicitly compute the vector space \(V\) and its three subspaces \(X,Y,Z\).
Abusing notation a little, let us write
$$ V = A \oplus B \oplus C \oplus D \oplus E \oplus F \oplus G $$
where now \(A, \dots, G\) denote the vector spaces assigned to the central dot by the quiver representations of the same name. Looking at the list above we see that \(A, B, C, D, E\) and \(F\) are 1-dimensional while \(G\) is 2-dimensional. So,
$$ V \cong \mathbb{R}^8 .$$
The next step is to determine the 3 subspaces \(X,Y,Z \subset V\).
We need a bit more notation to name all the subspaces associated to the quiver representation \(G\):

We are calling the copy of \(\mathbb{R}^2\) here \(G\). Let us denote the three copies of \(\mathbb{R}\) by \(G_1, G_2,\) and \(G_3\), starting at the top and going around clockwise:
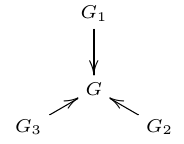
The vector space $G$ is 2-dimensional, while $G_1, G_2, G_3$ are 1-dimensional and distinct, so
$$ G_1 \vee G_2 = G_2 \vee G_3 = G_3 \vee G_1 = G $$
and
$$ G_1 \wedge G_2 = G_2 \wedge G_3 = G_3 \wedge G_1 = \{0\} . $$
We can now determine the subspaces \(X,Y,Z \subset V\). The subspace \(X\) is the direct sum of the vector spaces assigned to the top dot of the \(\mathbb{D}_4\) quiver by all 7 quiver representations under consideration. So, using the notation we have set up,
$$ X = A \oplus E \oplus F \oplus G_1 .$$
Similarly
$$ Y = B \oplus D \oplus F \oplus G_2 $$
and
$$ Z = C \oplus D \oplus E \oplus G_3 .$$
Using these facts we can work out the subspace of
$$ V = A \oplus B \oplus C \oplus D \oplus E \oplus F \oplus G \cong \mathbb{R}^8 $$
corresponding to any element of the lattice generated by $X,Y,Z$. For example, we have
$$ X \wedge Y = ( A \oplus E \oplus F \oplus G_1) \wedge (B \oplus D \oplus F \oplus G_2) = F$$
where we used the fact that $G_1 \wedge G_2 = \{0\}$.
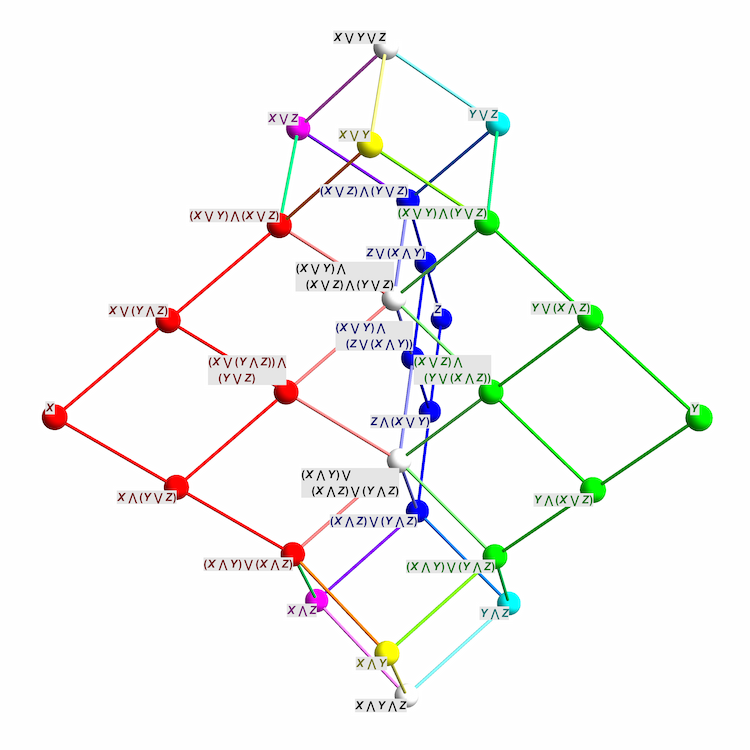
Greg Egan has summarized the results in this chart:
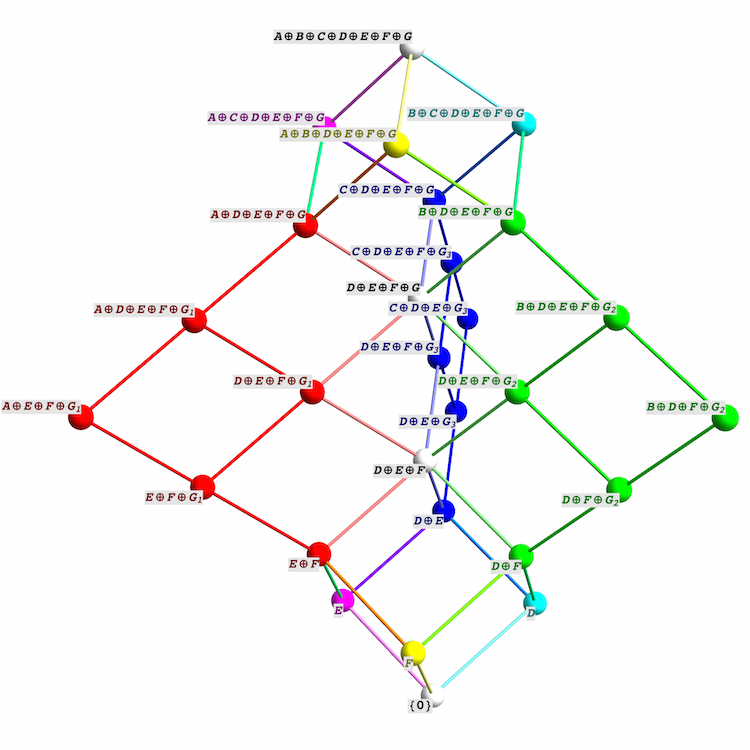
Tim Silverman prepared this table of the results:
$$\array{
\textrm{dimension 8:} \\
X\vee Y\vee Z&A\oplus B\oplus C\oplus D\oplus E\oplus F\oplus
G\\
\\
\textrm{dimension 7:} \\
X\vee Y&A\oplus B\oplus D\oplus E\oplus F\oplus G\\
X\vee Z&A\oplus
C\oplus D\oplus E\oplus F\oplus G\\
Y\vee Z&B\oplus C\oplus D\oplus
E\oplus F\oplus G\\
\\
\textrm{dimension 6:} \\
(X\vee Y)\wedge (X\vee Z)&A\oplus D\oplus E\oplus F\oplus G\\
(X\vee Y)\wedge (Y\vee Z)&B\oplus D\oplus E\oplus F\oplus G\\
(X\vee Z)\wedge (Y\vee Z)&C\oplus D\oplus E\oplus F\oplus G\\
\\
\textrm{dimension 5:} \\
(X\vee Y)\wedge (X\vee Z)\wedge (Y\vee Z)&D\oplus E\oplus F\oplus G\\
X\vee (Y\wedge Z)&A\oplus D\oplus E\oplus F\oplus G_1\\
Y\vee (X\wedge Z)&B\oplus D\oplus E\oplus F\oplus G_2\\
Z\vee (X\wedge Y)&C\oplus D\oplus E\oplus F\oplus G_3\\
\\
\textrm{dimension 4:} \\
(X\vee (Y\wedge Z)\wedge (Y\vee Z)&D\oplus
E\oplus F\oplus G_1\\
(Z\vee (X\wedge Y))\wedge (X\vee Y)&D\oplus E\oplus
F\oplus G_3\\
(Y\vee (X\wedge Z))\wedge (X\vee Z)&D\oplus E\oplus F\oplus
G_2\\
X&A\oplus E\oplus F\oplus G_1\\
Y&B\oplus D\oplus F\oplus G_2\\
Z&C\oplus D\oplus E\oplus G_3\\
\\
\textrm{dimension 3:} \\
(X\wedge Y)\vee (X\wedge Z)\vee (Y\wedge Z)&D\oplus E\oplus F\\
X\wedge (Y\vee Z)&E\oplus F\oplus G_1\\
Y\wedge (X\vee Z)&D\oplus F\oplus G_2\\
Z\wedge (X\vee Y)&D\oplus E\oplus G_3\\
\\
\textrm{dimension 2:} \\
(X\wedge Y)\vee (X\wedge Z)&E\oplus F\\
(X\wedge Y)\vee (Y\wedge Z)&D\oplus F\\
(X\wedge Z)\vee (Y\wedge Z)&D\oplus E\\
\\
\textrm{dimension 1:} \\
X\wedge Y&F\\
X\wedge Z&E\\
Y\wedge Z&D\\
\\
\textrm{dimension 0:} \\
X\wedge Y \wedge Z& \{0\}
}$$
Since all 28 of these subspaces are distinct, the lattice generated by \(X,Y,\) and \(Z\) is the same as the free modular lattice on 3 generators with \(\top\) and \(\bot\) removed: that is, Dedekind’s original lattice. One can check that Dedekind’s lattice does not embed in the lattice of subspaces of a space of dimension \(\lt 8\), because the corresponding quiver representation needs to contain copies of all 7 quiver representations \(A,\dots, G\), or extra relations would hold.
Puzzle 1. Is it a coincidence that \(V\) is 8-dimensional and the \(\mathrm{D}_4\) quiver is associated to the \(\mathfrak{so}(8)\) Lie algebra? There is no obvious relation visible in the argument above.
Puzzle 2. Is it a coincidence that Dedekind’s lattice has 28 elements and \(\mathfrak{so}(8)\) is 28-dimensional? Again this relation plays no obvious role in the argument above.
As a hint for Puzzle 2, Hugh Thomas pointed out that the portion of the free modular lattice on 3 generators above the middle rank is isomorphic to the poset of positive roots of \(\mathfrak{so}(4)\), with its usual ordering. This poset has 12 elements. Similarly, we can identify the portion below the middle rank with the poset of negative roots. The reason for this is unclear, and this leaves the middle rank somewhat mysterious: it has \(30 – 12 – 12 = 6\) elements. The Lie algebra \(\mathfrak{so}(4)\) is spanned by the positive roots, the negative roots, and its Cartan subalgebra, so its Cartan subalgebra has dimension \(28 – 12 – 12 = 4\).
For Dedekind’s original paper, see:
• Richard Dedekind, Über die von drei Moduln erzeugte Dualgruppe, Mathematische Annalen 53 (1900), 371–403.
For the four subspace problem, see:
• I. M. Gelfand, and V. A. Ponomarev, Problems of linear algebra and classification of quadruples of subspaces in a finite-dimensional vector space, Coll. Math. Spc. Bolyai 5 (1970), 163–237.
To see the difficulty with the problem, note that starting with 4 generically chosen points on a plane, and repeatedly drawing lines through points and creating new points by intersecting lines, one can generate infinitely many points and lines. Viewing this in terms of projective geometry, it follows that starting with 4 generically chosen 2-dimensional subspaces in \(\mathbb{F}^3\), where \(\mathbb{F}\) is an infinite field, one can generate infinitely many subspaces using \(\vee\) and \(\wedge\).
The new ideas in this post, if any, were obtained collaboratively in discussions here:
• John Baez, The free modular lattice on 3 generators, The n-Category Café, 19 September 2015.
• John Baez, How is the free modular lattice on 3 generators related to 8-dimensional space?, MathOverflow, 20 September 2015.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!



It seems as though this structure could be realizable (though not necessarily synthesizable) with carbon and hydrogen atoms. I wonder if anyone has tried?
Wow, I have no idea. There is a kind of subculture of people who try to synthesize chemicals based on mathematical concepts. Check out these:
• John Baez, Cubane, 5 March 2012.
• John Baez, Dodecahedrane, 5 March 2012.
However, I don’t think those people know about the free modular lattice on 3 generators!
This lattice, visually at least, greatly resembles an extended version of the free distributive lattice on three generators. If you cut out the middle layer of the free modular lattice and identify the corresponding elements of the adjacent two layers, you get the free distributive lattice. Do these lattices continue to be closely related for higher numbers of generators, and if so is there a clear way of stating the resemblance that doesn’t depend on the number of generators?
Intriguing questions!
Is there a picture somewhere of the free distributive lattice on 3 generators? Or a nice description of the free distributive lattice on \(n\) generators?
Since the modular identity is a weakened form of the distributive law, there is a lattice homomorphism from the free modular lattice on \(n\) generators to the free distributive lattice on \(n\) generators, say
$$ \alpha: \mathrm{FMod}_n \to \mathrm{FDist}_n $$
That must the reason for the resemblance you see. But since \(\alpha\) is onto, each element of \(\mathrm{FDist}_n\) corresponds to some subset of \(\mathrm{FMod}_n\): an equivalence class. That is, we get \(\mathrm{FDist}_n\) by ‘squashing down’ \(\mathrm{FMod}_n\).
So, ‘cutting out the middle layer’ is not the right way to think of what’s going on, but ‘identifying elements’ is.
With some work I could use this to take Egan’s labelled picture of the \(\mathrm{FMod}_3\), figure out which expressions become the same when we use the distributive law, and get a picture of \(\mathrm{FDist}_3\). But I don’t have the energy right now!
As mentioned in the blog article, the big difference between \(\mathrm{FMod}_3\) and \(\mathrm{FMod}_4\) is that the latter is infinite.
Is \(\mathrm{FDist}_n\) always finite? I seem to recall it is.
The free distributive lattice on $n$ generators is the lattice of monotone Boolean functions on $n$ variables, with conjunction and disjunction as the lattice operations. (Each generator maps to the function that outputs one of the variables and ignores the other variables.) There’s an image, with lattice elements labeled by the corresponding functions, at https://commons.wikimedia.org/wiki/File:Monotone_Boolean_functions.svg
Yes, this is what I mean too. I like how the weaker modular rule gives you a freer object, and enforcing the stricter distributive rule squashes the object down a bit. If you go to the wiki article on Dedekind numbers, you’ll see a nice picture of the lattice at the top right. The Dedekind numbers grow very fast, and there’s definitely some recursion involved, but as of right now there isn’t a closed formula. Also, the 4th Dedekind number turns out to be the 168. I’m really curious about how \(\mathrm{FMod}_4\) looks. Is it related to the modular group?
I don’t know what the free modular lattice on 4 generators looks like, but just as the free modular lattice is related to the 3 subspace problem as discussed here, the free modular lattice on 4 generators is related to the 4 subspace problem.
The 4 subspace problem asks to classify all ways one can choose 4 subspaces \(L_1, \dots, L_4\) of a finite-dimensional vector space \(L\), up to invertible linear transformations of \(L\). Any choice of 4 subspaces of a finite-dimensional vector spaces gives a ‘linear representation’ of the free modular lattice on 4 generators, and two such representations are equivalent if they differ by an invertible linear transformation of \(L\).
The 4 subspace problem is famous for being “wild”, unlike the 3 subspace problem. This is related to the free modular lattice on 4 generators being infinite.
If you can get ahold of it, the classical reference is here:
• I. M. Gelfand and V. A. Ponomarev, Problems of linear algebra and classification of quadruples of subspaces in a finite-dimensional vector space, Coll. Math. Spc. Bolyai 5 (1970), 163–237.
It seems easier to get ahold of this paper, since it’s free online:
• Rafael Stekolshchik, Gelfand–Ponomarev and Herrmann constructions for quadruples and sextuples, Journal of Pure and Applied Algebra 211 (2007), 95–202.
I think it will give you a rough idea of what’s going on, though it’s mainly about another problem involving 6 subspace. It quotes Gian-Carlo Rota as saying
This is from Rota’s article “Ten mathematics problems I will never solve”.
By the way, you have to be careful, because the classification of linear representations of a modular lattice depends on a choice of field, while the free modular lattice on \(n\) generators does not. Worse, it’s possible that when \(n\) is large enough there are distinct elements of the free modular lattice on \(n\) generators that cannot be distinguished by any linear representation. I forget the story here, but I seem to recall reading something about this.
It looks like if you identify nodes up to the logical biconditional, you get a picture that looks like this:
https://upload.wikimedia.org/wikipedia/commons/thumb/5/57/Monotone_Boolean_functions_0%2C1%2C2%2C3.svg/400px-Monotone_Boolean_functions_0%2C1%2C2%2C3.svg.png
And these are counted by Dedekind numbers. Apparently only the first 8 Dedekind numbers are known. I wonder if this could shed some light.
I don’t know what you mean by ‘identify nodes up to the logical biconditional’, since two elements \(a,b\) of a modular lattice both imply each other iff they are equal.
I’m suspecting that you’re actually replacing the free modular lattice on \(n\) generators, \(\mathrm{FMod}_n\) by the lattice of monotone functions \(f : \mathrm{FMod}_n \to \{0,1\} \). If I remember correctly, this is the same as the lattice of ideals of \(\mathrm{FMod}_n\). And if I remember correctly, this construction—replacing a lattice by its lattice of ideals—is equivalent to taking that lattice and forcing it to be distributive, by identifying expressions that become equal when you get to use the distributive law.
If I’m right, then, you’re taking \(\mathrm{FMod}_n\) and performing a quotient (just as mentioned in David Eppstein’s comment) to get \(\mathrm{FDist}_n\).
One big piece of evidence for my guesses here is that the \(n\)th Dedekind number is the number of elements of \(\mathrm{FDist}_n\)!
(By the way, an irksome feature of this blog is that even I cannot get pictures to appear in comments. On my other WordPress blog I can: other people can’t make images appear in comments, perhaps as an anti-spam feature, but if they include the links I can make the images appear. But on this one, despite the name Visual Insight, I cannot! This blog is run by the American Mathematical Society, so I should force someone there to fix this.)
I also don’t know what “up to the logical biconditional” means but I think the identification of nodes that turns this into the free distributive lattice is the following. At the center of the diagram there are five lattice elements forming a $K_{2,3}$ subgraph. Collapse the six edges of this subgraph, and also collapse another six edges parallel to the first six (where by two edges being parallel I mean that they are two opposite sides of a 4-cycle). So the central five elements of the modular lattice map to a single central element of the distributive lattice (the majority function) and six more pairs of elements of the modular lattice have the same image as each other in the distributive lattice.
The six identified pairs end up being instances of the distributive law (in retrospect, unsurprisingly) e.g. $x\vee(y\wedge z)=(x\vee y)\wedge(x\vee z)$. The identification of the five in the middle is messier when expressed algebraically, though.
Following your invitation, I’ll make an attempt to comment here as if that was the same as commenting on G+… what incites me first to pack together random comments I’d most likely have interjected separately on a social network comment stream:
(1) The rotating image is reminiscent of a Crookes radiometer.
(2) Does the “three” in “free lattice on three generators” deserve taking as a hint that the latter could serve in a narrative about the color force?
The article http://web.mst.edu/~insall/Research/Algebra%20and%20Nonstandard%20Algebra/Lattices/Geom/Geometric%20Conditions%20for%20Local%20Finiteness.pdf gave a simple argument that the lattice of closed convex sets in the plane is not modular, by finding three closed segments A, B, and C that generate an infinite lattice of closed convex subsets of the plane. Near the end of the article, a conjecture is made about locally finite lattices of closed convex subsets of Hilbert Spaces, but that conjecture has not borne up under scrutiny.
Interesting!