This image by intocontinuum show how you can take 8 perfectly rigid regular tetrahedra and connect them along their edges to form a ring that you can turn inside-out. This is called a kaleidocycle, and you can actually form a kaleidocycle with any even number of tetrahedra, as long as you have at least 8.
You can see kaleidocycles with 8, 10, and 12 tetrahedra here:
• Intothecontinuum, An even number of (at least 8) regular tetrahedra…, Archery, 19 May 20123.
and this is where I got my picture. If you attempt to create a kaleidocycle with just 6 tetrahedra, the tetrahedra collide and intersect each other as they move, as shown in these animations by Greg Egan:
• Greg Egan, Collidocycle: side view and top view.
You can also make kaleidocycles out of paper:
• Jürgen Köller, Kaleidocycles, Mathematische Basteleien.
This website shows a variety of other flexible polyhedra, as well. For example, there’s a ring of 16 pyramids, all congruent, that folds up into a perfect regular tetrahedron. And there’s another made of 16 pyramids, all congruent, that folds into an octahedron!
The Rigidity Theorem says if the faces of a convex polyhedron are made of a rigid material and the polyhedron edges act as hinges, the polyhedron can’t change shape at all: it’s rigid. The kaleidocycles show this isn’t true for a polyhedron with a hole in it.
Of course, having a hole is an extreme case of being nonconvex. And in fact there are nonconvex polyhedra without a hole that aren’t rigid! The first of these was discovered by Robert Connelly in 1978. Connelly’s polyhedron has 18 triangular faces. Later, Klaus Steffen found a flexible polyhedron with just 14 triangular faces. You can see it in motion here, along with a detailed description of how it works:
• Greg Egan, Steffen’s polyhedron.
Later, Maksimov proved that Steffen’s polyhedron is the simplest flexible polyhedron with just triangular faces:
• I. G. Maksimov, Polyhedra with bendings and Riemann surfaces, Uspekhi Matemat. Nauk 50 (1995), 821–823.
In 1997, Connelly, Sabitov and Waltz proved something even more impressive: the Bellows Conjecture. This says that a polyhedron that’s not rigid must keep the same volume as you flex it!
The famous mathematician Cauchy had claimed to prove the Rigidity Theorem in 1813. But there was a mistake in his proof. Nobody noticed it for a long time. It seems mathematician named Steinitz spotted the mistake and fixed it in a 1928 paper.
Puzzle 1: What was the mistake?
Alexander Gaifullin has generalized the Rigidity Theorem and Bellows Conjecture to higher-dimensional convex polytopes. It’s also been shown that ‘generically’ polyhedra are rigid, even if they’re not convex.
So, there are lots of variations on this theme: it’s very flexible.
Puzzle 2: Can you make higher-dimensional kaleidocycles out of higher-dimensional regular polytopes? For example, a regular 5-simplex has 6 corners; if you attach 3 corners of one to 3 corners of another, and so on, maybe you can make a flexible ring. Unfortunately this is in 5 dimensions—a 4-simplex has 5 corners, which doesn’t sound so good, unless you leave one corner hanging free, in which case you can just take the movie here and imagine it as the ‘bottom’ of a 4d movie where each tetrahedron is the ‘base’ of a 4-simplex: sorta boring.
For more, see:
• Flexible polyhedra, Wolfram Mathworld.
• Cauchy’s theorem (geometry), Wikipedia.
The Bellows Conjecture was generalized to higher dimensions here:
• Alexander A. Gaiufullin, Generalization of Sabitov’s theorem to polyhedra of arbitrary dimensions, 19 October 2015.
and to higher-dimensional hyperbolic spaces here:
• Alexander A. Gaifullin, The analytic continuation of volume and the Bellows conjecture in Lobachevsky spaces, 22 August 2015.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!

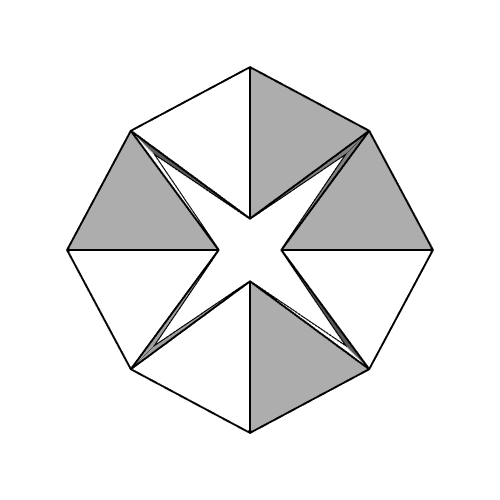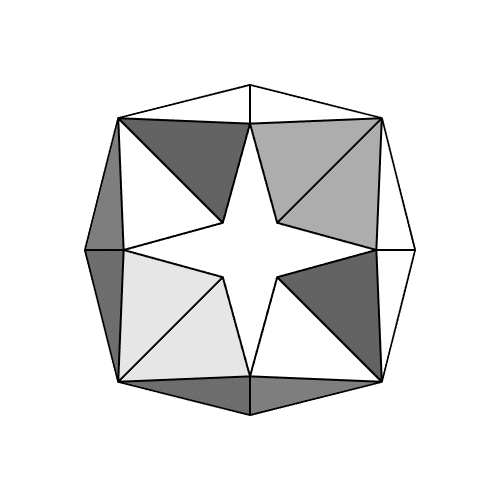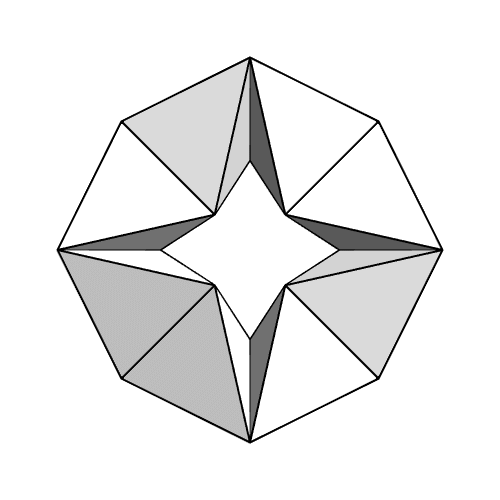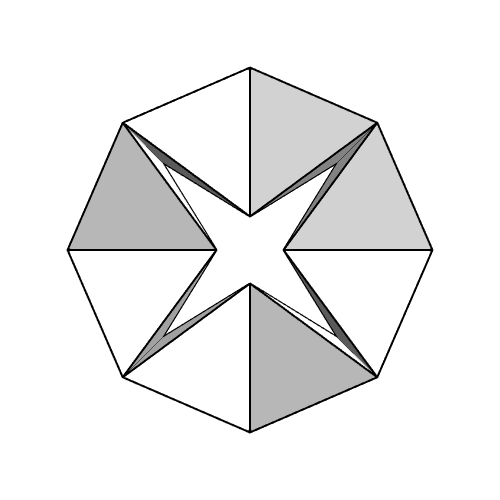



John, there are many Kaleidocycles to explore by folding circles without using polygon formulas.
Check out
https://www.youtube.com/watch?v=n5QWFD4xBqA
https://www.youtube.com/watch?v=boZjbsMCCZo
https://www.facebook.com/wholemovement/videos
Cool! Those videos are nice.