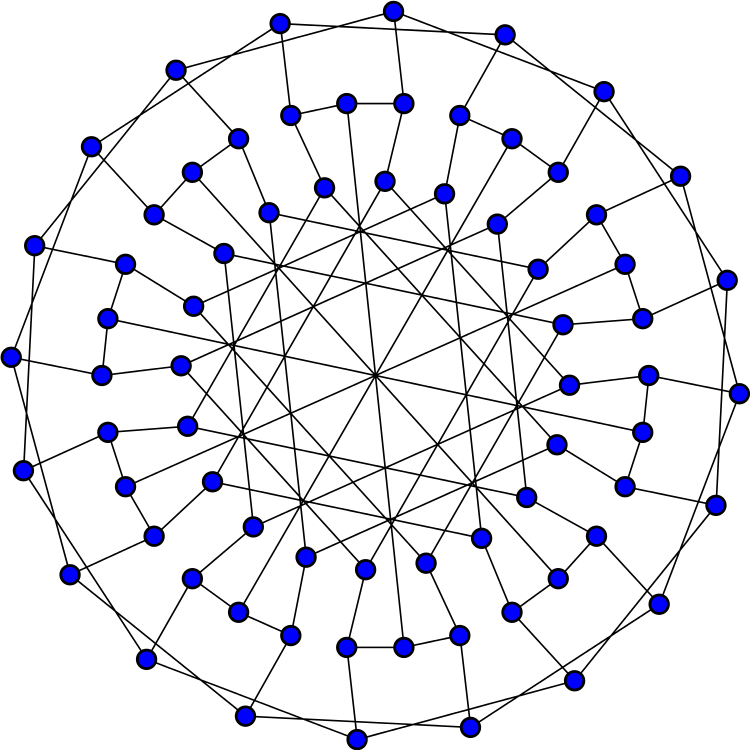
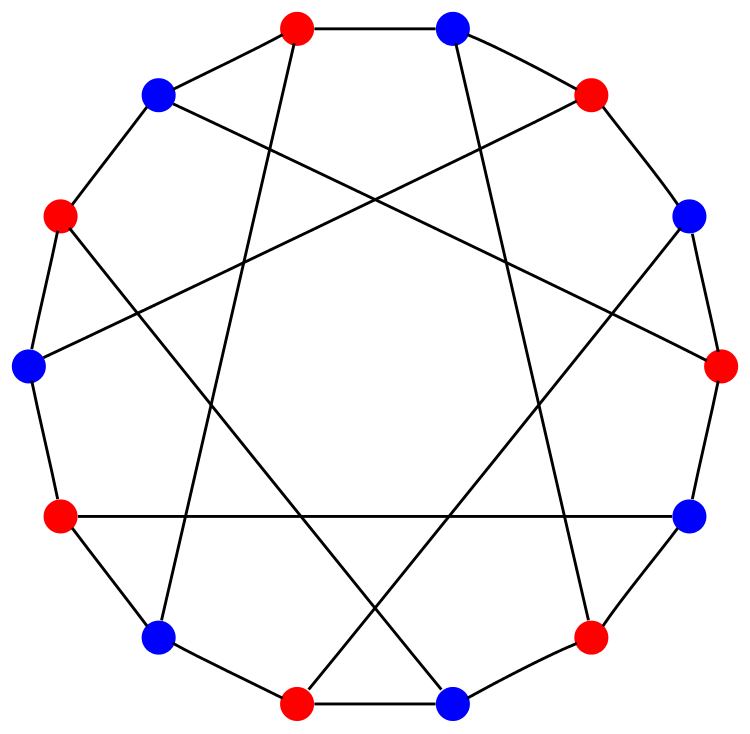
This is the Balaban 10-cage, the first known (3,10)-cage. An \((r,g)\)-cage is graph where every vertex has \(r\) neighbors, the shortest cycle has length at least \(g\), and the number of vertices is minimal given these constraints. The Balaban 10-cage has 70 vertices, 105 edges, and a symmetry group of order 80, which does not act transitively on the nodes or edges of this graph.

It is easy to see that \((r,g)\)-cages are uninteresting for \(r \lt 3\). There exists at least one \((3,g)\)-cage for any \(g \ge 3\). For low values \(g\) we have discussed many of these \((3,g)\)-cages already on Visual Insight—click the links to see them:

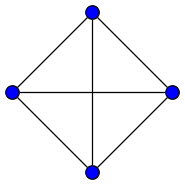
• The only (3,3)-cage is \(K_4\), the complete graph on 4 vertices, having an edge between each pair of distinct vertices.

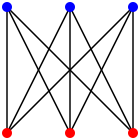
• The only (3,4)-cage is \(K_{3,3}\), the complete bipartite graph with 3 red vertices and 3 blue vertices and an edge between each red vertex and each blue vertex.

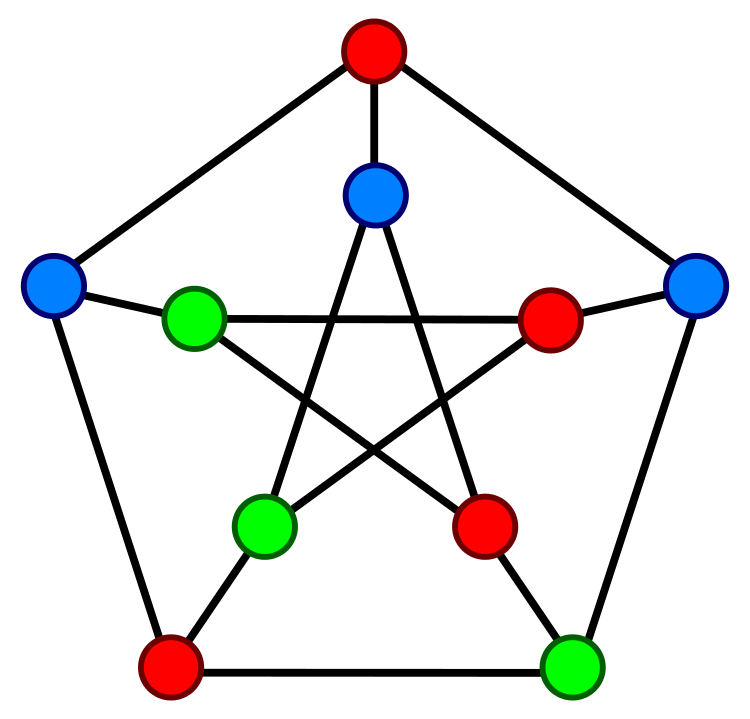
• The only (3,5)-cage is the Petersen graph.

• The only (3,6)-cage is the Heawood graph.

• The only (3,7)-cage is the McGee graph.

• The only (3,8)-cage is the Tutte–Coxeter graph.

• There are 18 nonisomorphic (3,9)-cages.

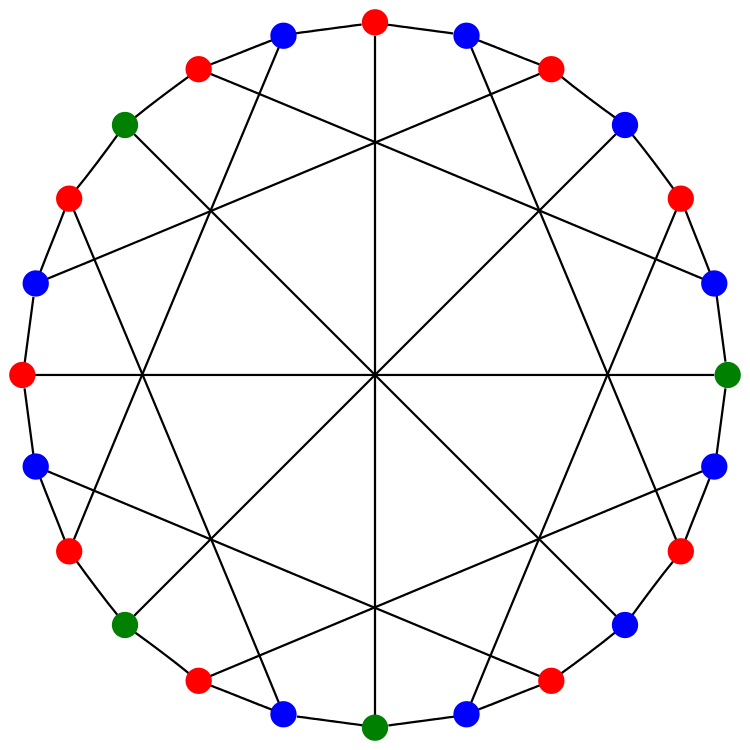
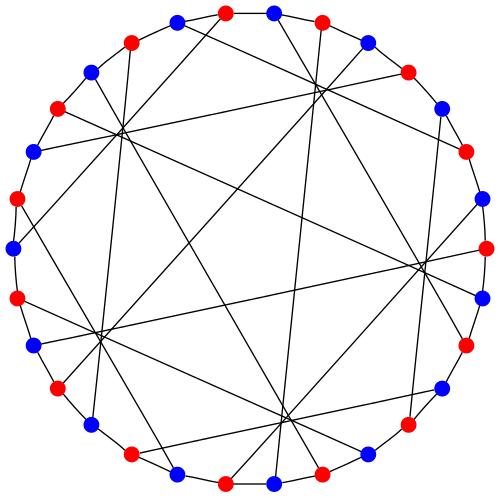
• There are 3 nonisomorphic (3,10)-cages.

The Balaban 10-cage first appeared here:

• Alexandru T. Balaban, A trivalent graph of girth ten, J. Combin. Theory Ser. B 12 (1972), 1–5.

Balaban was working mostly on chemistry in this phase of his life, and later wrote:

In my spare time, I tried to solve graph-theoretical problems, and I became intrigued by the fact that trivalent cages were known for girths 3 to 8 and 12, but there was a gap for girths 9, 10, and 11. With symmetry as a guide and with my observation on how smaller cages can be obtained from larger cages I found a trivalent graph with 70 vertices and I conjectured that it was a 10-cage, but I did not publish this result until a few years later. Only much later was it proved to be indeed the first 10-cage (two other ones were discovered later) by mathematicians using arrays of computers working for long time; a similar computational effort proved that another conjectured trivalent graph with 112 vertices to be the unique 11-cage. Both these cages are known as “Balaban graphs”; the Balaban 10-cage appears on the cover of the book Pearls in Graph Theory by N. Hartsfield and G. Ringel. In an international effort that included Coxeter, Frucht, Harries, and Evans along with me, we had found several nice, highly symmetric graphs with 60 vertices and girth 9, but before anything was published about them, Norman Biggs published a paper about the first 9-cage with 58 vertices. It is now known that there are eighteen 9-cages, all with low symmetry.

This is from:

• Alexandru T. Balaban, Autobiographical notes: 80 years of age, 68 years of chemistry, MATCH Commun. Math. Comput. Chem. 66 (2011), 7–32.

For more on cages, see:

• Cage (graph theory), Wikipedia.

• Geoffrey Exoo and Robert Jajcay, Dynamic cage survey, Electronic Journal of Combinatorics, Dynamic Survey DS16 (2013).

• Mirka Miller and Jozef Sirán, Moore graphs and beyond: a survey of the degree/diameter problem, Electronic Journal of Combinatorics, Dynamic Survey DS14 (2013).

The layout for the featured picture comes from here:

• T. Pisanski, M. Boben, D. Maru, A. Orbani and A. Graovac, The 10-cages and derived configurations, Discrete Mathematics 275 (2004), 265–276.

The featured picture was created by Koko90 and put on Wikicommons under a Creative Commons Attribution-Share Alike 3.0 Unported license. For information on the other pictures, click the links, except for:

• the complete graph \(K_4\), which was drawn by Koko90 and put on Wikicommons under a Creative Commons Attribution-Share Alike 3.0 Unported license,

• the complete bipartite graph \(K_{3,3}\), which was drawn by -xfi- and put on Wikicommons under a Creative Commons Attribution-Share Alike 3.0 Unported license, and

• the Petersen graph, which was drawn by Chris Martin and placed into the public domain on Wikicommons.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!