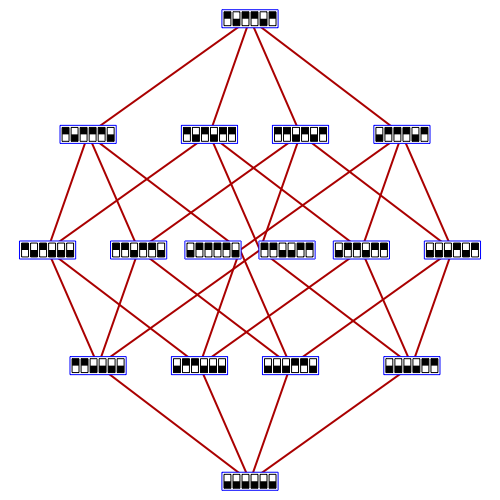
This picture by Greg Egan shows a hypercube with all vertices except the bottom labelled by duads, that is, 2-element subsets of a 6-element set. There are 15 duads, while the hypercube has 16 vertices.

In fact, we can think of this hypercube as a 4-dimensional vector space over the field with two elements, \(\mathbb{F}_2\). Even better, doing this gives a nice proof that \(S_6\), the symmetric group consisting of permutations of 6 letters, is isomorphic to \( \mathrm{Sp}(4,\mathbb{F}_2) \), the group of symplectic transformations of a 4-dimensional symplectic vector space over \(\mathbb{F}_2 \).

To see this, start with the 6-dimensional vector space \(\mathbb{F}_2^6\). Then form the 5-dimensional subspace consisting of vectors whose coordinates sum to zero:

$$ U = \{ v \in \mathbb{F}_2^6 : \; v_1 + \cdots + v_6 = 0 \} $$

Note that the vector

$$ u = (1,1,1,1,1,1) $$

lies in \(U\). Thus, we can form a 4-dimensional quotient space

$$ V = U/\langle u \rangle $$

In fact, all 15 nonzero vectors in \(V\) correspond to duads! To see this, note that there are four kinds of vectors in \(U\):

1. \( (0,0,0,0,0,0) \),
2. \( (1,1,0,0,0,0) \) and the vectors obtained from this by permuting coordinates,
3. \( (1,1,1,1,0,0) \) and the vectors obtained from this by permuting coordinates,
4. \( (1,1,1,1,1,1 )\).

Adding \(u\) to the vector of the first kind produces the vector of the last kind, and vice versa. Adding \(u\) to a vector of the second kind gives one of the third kind, and versa. So, in \(V = U/\langle u \rangle \), every vector is equivalent to one of the first or second kinds. But vectors of the second kind correspond naturally to duads. Thus, every nonzero vector in \(V\) corresponds naturally to a duad.

In the picture, Egan has somewhat arbitrary chosen a basis for \(V\) consisting of the equivalence classes of the vectors

$$ (1,1,0,0,0,0), \quad (0,1,1,0,0,0), \quad (0,0,0,1,1,0), \quad (0,0,0,0,1,1) $$

These form the second to bottom row in the hypercube, next to the origin. The other vectors are all linear combinations of these.

Even better, the original vector space \(\mathbb{F}_2^6\) has a symplectic structure on it, meaning a nondegenerate alternating bilinear form. This bilinear form

$$ \omega : \mathbb{F}_2^6 \times \mathbb{F}_2^6 \to \mathbb{F}_2 $$

is given by

$$ \omega((a,b,c,d,e,f), (a’,b’,c’,d’,e’,f’)) =
(ab’ – ba’) + (cd’ – dc’) + (ef’ – fe’) . $$

The minus signs are only to reassure readers familiar with symplectic structures in other contexts; over \(\mathbb{F}_2\) they have no effect. So, for any vector \(v = (a,b,c,d,e,f)\) we have

$$ \omega(u,v) = a + b + c + d + e + f $$

Thus, \(U\) consists of the vectors \(v\) with that are orthogonal to \(u\) in the sense that \(\omega(u,v) = 0\). In particular, \(u \in U\) is orthogonal to itself. Using these facts, one can check that the quotient space \(V = U/\langle u \rangle\) inherits a symplectic structure from \(\mathbb{F}_2^6\): if \([v],[w] \in V\) are equivalence classes, \(\omega(v,w)\) is independent of the choice of representatives \(v,w \in U\), and this defines a symplectic structure on \(V\). This process of taking a symplectic structure and getting one on a quotient space of a subspace is an example of ‘symplectic reduction’.

The group of linear transformations preserving the symplectic structure on a 4-dimensional symplectic vector space over the field \(\mathbb{F}_2\) is called the symplectic group \(\mathrm{Sp}(4,\mathbb{F}_2)\), or \(\mathrm{Sp}(4,2)\) for short. This acts on \(V\), and thus acts as permutations of the 15 duads.

The group \(S_6\) acts by permutation of coordinates on \(V\), so it too acts to permute the 15 duads. This suggests that perhaps

$$ S_6 \cong \mathrm{Sp}(4,\mathbb{F}_2) $$

and indeed this is true. There are various ways to see this.

One method is to note that the action of \(S_6\) by permuting coordinates on \(V\) preserves the symplectic structure on \(V\). This gives a homomorphism

$$ S_6 \to \mathrm{Sp}(4,\mathbb{F}_2) $$

This homomorphism is 1-1 because every nontrivial permutation in \(S_6\) acts nontrivially on duads, which correspond to nonzero elements of \(V\). To check that it is onto, it suffices to show both groups have the same number of elements. The group \(S_6\) has \(6! = 720\) elements, while for symplectic groups we have this general formula:

$$ \vert \mathrm{Sp}(2m,\mathbb{F}_q)\vert = \prod_{i = 1}^m (q^{2i} – 1)q^{2i-1} $$

which gives

$$ \vert\mathrm{Sp}(4,\mathbb{F}_2)\vert = (2^2 – 1)2^1 \cdot (2^4 – 1)2^3 = 3 \cdot 2 \cdot 15 \cdot 8 = 720 . $$

A more conceptual approach, which inspired the more plodding one above, was offered by Tim Silverman on the n-Category Café. Silverman focuses on the projective symplectic group \(\mathrm{PSp}(4,\mathbb{F}_2)\), formed by taking the symplectic group and modding out by invertible scalars. However, since 1 is the only invertible element of \(\mathrm{F}_2\), this is the same as \(\mathrm{Sp}(4,\mathbb{F}_2)\). He writes:

Here is how \(S_6\) is isomorphic to \(\mathrm{\mathrm{PSp}}(4, \mathbb{F}_2)\).

Take a \(6\)-dimensional vector space over \(\mathbb{F}_2\): say sextuples of ones and zeros. Take the subspace orthogonal to \(\left(1,1,1,1,1,1\right)\), getting a 5-dimensional space, consisting of sextuples with an even number of ones. Then take the quotient by addition of \(\left(1,1,1,1,1,1\right)\), getting a \(4\)-dimensional space.

Now think of this in another way: the first space is the set of subsets of a set \(S\) of \(6\) elements corresponding to coordinates (for each each vector, take the subset of coordinates consisting of those with a component value of \(1\)). The \(5\)-dimensional subspace consists of subsets of even cardinality. The quotient identifies subsets with their complements. Sum of vectors is symmetric difference of sets.

There are two types of element in the \(4\)-dimensional space: the identity, consisting of the equivalence class

$$ \left\{\left(0,0,0,0,0,0\right), \left(1,1,1,1,1,1\right)\right\}, $$

or, in the alternative formulation the empty set together the whole of \(S\); and the other elements, all of which are two-element equivalence classes containing a \(2\)-element subset of \(S\) together with its \(4\)-element complement.

If we go over to projective space, all we do is throw away the origin (because \(\mathbb{F}_2\) only has one non-zero scalar, making everything very simple). This gives us a space whose points are duads.

The vector sum of two duads depends on their overlap. Letting \(a, b, c, d, e\) and \(f\) be the elements of \(S\) in some order:

• \((ab)+(ab) =0\), e.g.

$$ \left(1,1,0,0,0,0\right)+\left(1,1,0,0,0,0\right)=\left(0,0,0,0,0,0\right). $$

• \((ab)+(bc)=(ac)\), e.g.

$$\left(1,1,0,0,0,0\right)+\left(0,1,1,0,0,0\right)=\left(1,0,1,0,0,0,0\right) .$$

• \((ab)+(cd)=(ef)\), e.g.

$$\left(1,1,0,0,0,0\right)+\left(0,0,1,1,0,0\right)=\left(1,1,1,1,0,0\right) \sim \left(0,0,0,0,1,1\right). $$

Then, in the projective space there are two kinds of line, of the form \(\left\{(ab),(bc),(ac)\right\}\) and \(\left\{(ab),(cd),(ef)\right\}\) respectively.

Now there is a symplectic structure on the duads given by parity of overlap:

$$ \omega((ab),(ab))=0 $$

$$ \omega(ab),(bc)) =1 $$

$$ \omega((ab),(cd)) =0 $$

An example symplectic basis would be \(\left\{(ab),(bc),(de),(ef)\right\}\).

Since both the vector space (or projective space) structure and the symplectic structure depend only on the overlap between pairs, it’s not hard to see that the symplectic group must be \(S_6\). The two types of lines are the non-isotropic and isotropic lines respectively. (That is, lines of the form \(\left\{(ab),(bc),(ac)\right\}\) have all their points mutually non-orthogonal, and lines of the form \(\left\{(ab),(cd),(ef)\right\}\) have all their points mutually orthogonal.)

Thus (necessarily isotropic) points are duads, and isotropic lines are synthemes, explaining why the duads and synthemes with the obvious incidence relation form a generalised quadrangle.

It’s a bit tedious to work out, but planes consist of a distinguished duad, together with the \(6\) duads formed from the \(4\) elements of \(S\) not lying in the distinguished duad. The distinguished duad is then the pole of the plane (i.e. the unique point orthogonal to everything in the plane).

These planes are, of course, Fano planes.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!