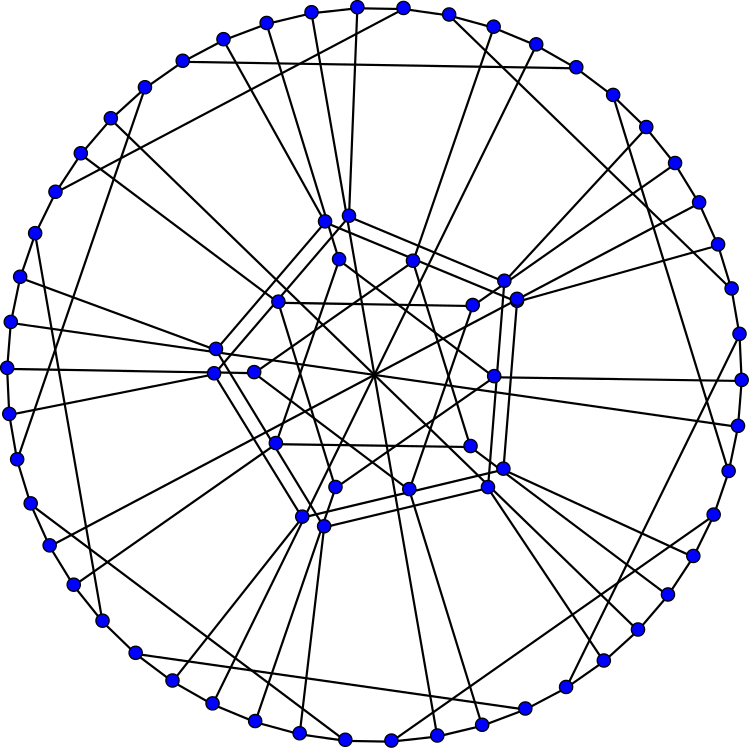
This is the Harries graph. It is a graph with the minimum number of vertices such that each vertex is connected to 3 others and every cycle has length at least 10. Such graphs are called (3,10)-cages.
There are just three (3,10)-cages. We have already mentioned one:
• Balaban 10-cage, Visual Insight.
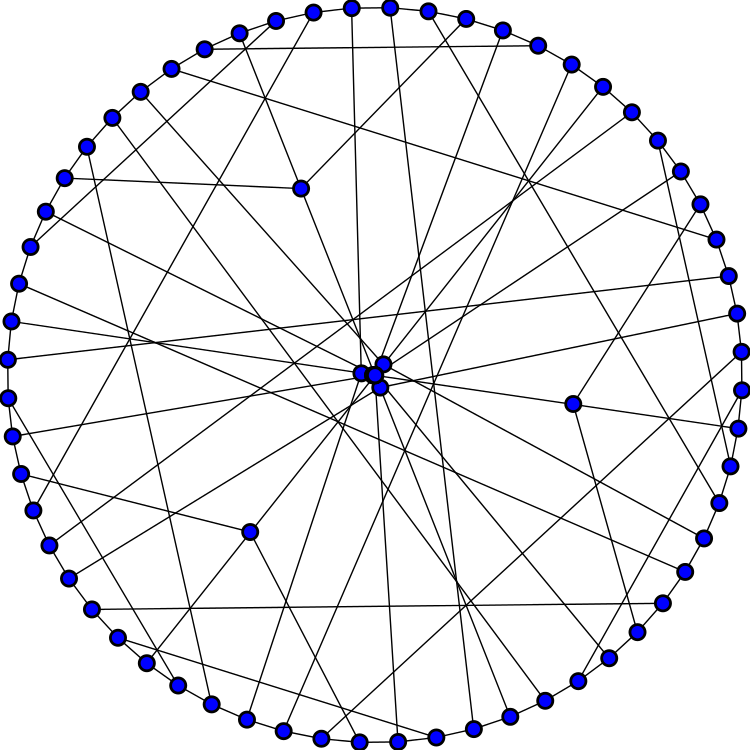
The Harries graph has a closer resemblance to the third (3,10)-cage, the Harries-Wong graph:
Namely, the Harries graph and Harries–Wong graph are ‘isospectral’. Any simple graph has an adjacency matrix, a square matrix where is the number of edges from the th node to the th node. Two graphs with same number of nodes are isospectral if their adjacency matrices have the same eigenvalues, counted with multiplicity.
We can also associate an operator to a graph called the graph Laplacian, a discretized version of the ordinary Laplacian. Two simple graphs are isospectral iff their graph Laplacians have the same eigenvalues, counted with multiplicity. For more details, see:
• Spectral graph theory, Wikipedia.
• Andries E. Brouwer and Willem H. Haemers Spectra of Graphs, Springer, Berlin, 2011.
The layout for these pictures come from here:
• T. Pisanski, M. Boben, D. Maru, A. Orbani and A. Graovac, The 10-cages and derived configurations, Discrete Mathematics 275 (2004), 265–276.
The picture of the Harries graph was created by Koko90 and put it on Wikicommons under a Creative Commons Attribution-Share Alike 3.0 Unported license. Koko90 also created the picture of the Harries–Wong graph and put it on Wikicommons under the same license.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!




What graph properties distinguish the three 10-cages?
You mean apart from the fact that they’re not isomorphic as graphs?
All 3 graphs have 70 vertices, 105 edges, chromatic number 2, chromatic index 3, radius 6, diameter 6, girth 10. They’re all Hamiltonian. The Harries graph and Harries–Wong graph are isospectral, so they also have the same characteristic polynomial. The Balaban 10-cage does not.
So, I guess the interesting question is: what’s different about the Harries graph and Harries–Wong graph?