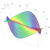
This is the {6,3,5} honeycomb, drawn by Roice Nelson.
A 3-dimensional honeycomb is a way of filling 3d space with polyhedra or infinite sheets of polygons. Besides honeycombs in 3d Euclidean space, we can also have honeycombs in 3d hyperbolic space, a non-Euclidean geometry with constant negative curvature. The {6,3,5} honeycomb lives in hyperbolic space.
The {6,3,5} honeycomb is also called the order 5 hexagonal tiling honeycomb. The reason is that it’s built from flat planes tiled by regular hexagons, and 5 of these planes meet along each edge of the honeycomb. It is worth comparing the {6,3,3} and {6,3,4} honeycombs, where fewer planes tiled by hexagons meet along each edge:
• {6,3,3} honeycomb, Visual Insight.
• {6,3,4} honeycomb, Visual Insight.
All these honeycombs are paracompact: instead of polyhedra, they contain infinite sheets tiled by polygons (which happen to be hexagons).
The notation {6,3,5} is an example of a Schläfli symbol. The Schläfli symbol is defined in a recursive way. The symbol for the hexagon is {6}. The symbol for the hexagonal tiling of the plane is {6,3} because 3 hexagons meet at each vertex. Finally, the hexagonal tiling honeycomb has symbol {6,3,5} because 5 hexagonal tilings meet at each edge.
Just as the {6,3} inside {6,3,5} describes the hexagonal tilings inside the {6,3,5} honeycomb, the {3,5} describes the vertex figure of this honeycomb: that is, the way the edges at each vertex. {3,5} is the Schläfli symbol for the regular icosahedron, and if you look very carefully at the picture you can can see that each vertex has 12 edges coming out, just like the edges going from the center of an icosahedron to its corners.
The Coxeter diagram of the {6,3,5} honeycomb is
For more on what this means, see the above Visual Insight articles on honeycombs: they all work roughly the same way. And for more on this particular honeycomb and its close relatives, see:
• Order-5 hexagonal tiling honeycomb, Wikipedia.
Puzzle: Say you start at one vertex in this picture, a place where edges meet. Say you randomly choose an edge and walk down it to the next node… each edge being equally likely. Say you keep doing this. This is the most obvious random walk you can do on the {6,3,5} honeycomb. Is the probability that eventually you get back where you started equal to 1? Or is it less than 1?
If that’s too hard, try the same sort of question with the usual cubical honeycomb in ordinary flat 3d space. Or the square lattice on the plane! Or the integer lattice on the real line!
Puzzle: The symmetry group of 3d hyperbolic space, not counting reflections, is PSL(2,C). Can you explicitly describe the subgroup that preserves the order-5 hexagonal tiling honeycomb?
Roice Nelson, the creator of this image, has a blog with lots of articles about geometry, and he makes plastic models of interesting geometrical objects using a 3d printer:
• Roice.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!