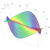
This is the {6,3,4} honeycomb, drawn by Roice Nelson.

A 3-dimensional honeycomb is a way of filling 3d space with polyhedra or infinite sheets of polygons. Besides honeycombs in 3d Euclidean space, we can also have honeycombs in 3d hyperbolic space, a non-Euclidean geometry with constant negative curvature. The {6,3,4} honeycomb lives in hyperbolic space.

How do you build this structure? Make 3 intersecting rods at right angles to each other. Make lots of copies of this thing. Then stick them together so that as you go around from one intersection to the next, following the rods, the shortest possible loop is always a hexagon!

This is impossible in ordinary flat 3-dimensional space. You can only succeed if the shortest possible loop is a square. Then you get the familiar cubic lattice:

To get hexagons instead of squares, space needs to be curved! You can succeed if you work in hyperbolic space, where it’s possible to create a hexagon whose internal angles are all 90°. In ordinary flat space, only a square can have all its internal angles be 90°.

The {6,3,4} honeycomb is also called the order 4 hexagonal tiling honeycomb. The reason is that it contains sheets tiled by regular hexagons — you can see one in the middle of the picture — 4 of these sheets meet along each edge of the honeycomb. It is worth comparing the {6,3,3} honeycomb, where 3 planes tiled by hexagons meet along each edge:

• {6,3,3} honeycomb, Visual Insight.

Both these honeycombs are paracompact: instead of polyhedra, they contain infinite sheets tiled by polygons. There are 15 regular honeycombs in 3d hyperbolic space, of which 11 are paracompact. For more, see:

• Paracompact uniform honeycomb, Wikipedia.

The notation {6,3,4} is an example of a Schläfli symbol. The Schläfli symbol is defined in a recursive way. The symbol for the hexagon is {6}. The symbol for the hexagonal tiling of the plane is {6,3} because 3 hexagons meet at each vertex. Finally, the hexagonal tiling honeycomb has symbol {6,3,4} because 4 hexagonal tilings meet at each edge.

Just as the {6,3} inside {6,3,4} describes the hexagonal tilings inside the {6,3,4} honeycomb, the {3,4} describes the vertex figure of this honeycomb: that is, the way the edges at each vertex. {3,4} is the Schläfli symbol for the regular octahedron, and if you look at the picture you can can see that each vertex has 6 edges coming out, just like the edges going from the center of an octahedron to its corners.

The Coxeter diagram of the {6,3,4} honeycomb is

 

The symmetry group of the {6,3,4} honeycomb is a discrete subgroup of the symmetry group of hyperbolic space. This discrete group has generators and relations summarized by the unmarked Coxeter diagram:

 

This diagram says there are four generators $s_1, \dots, s_4$ obeying relations encoded in the edges of the diagram:

$$ (s_1 s_2)^6 = 1 $$
$$ (s_2 s_3)^3 = 1 $$
$$ (s_3 s_4)^4 = 1 $$

together with relations

$$s_i^2 = 1$$

and

$$ s_i s_j = s_j s_i \; \textrm{ if } \; |i – j| > 1 $$

Marking the Coxeter diagram in different ways lets us describe many honeycombs with the same symmetry group as the hexagonal tiling honeycomb—in fact, $2^4 – 1 = 15$ of them, since there are 4 dots in the Coxeter diagram! You can see some of these uniform honeycombs here:

• Order-4 hexagonal tiling honeycomb, Wikipedia.

Puzzle: The symmetry group of 3d hyperbolic space, not counting reflections, is $\mathrm{PSL}(2,\mathbb{C})$. Can you explicitly describe the subgroup that preserves the order-4 hexagonal tiling honeycomb?

Roice Nelson, the creator of this image, has a blog with lots of articles about geometry, and he makes plastic models of interesting geometrical objects using a 3d printer:

• Roice.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!