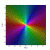
Atomic Singular Inner Function with Atoms at Fifth Roots of Unity –
Elias Wegert, www.visual.wegert.com

This picture, drawn by Elias Wegert, uses colors to show the phase $f/|f|$ of the complex function

$$f(z) = \prod_{k=1}^5 \exp\left(\frac{z+\omega^k}{z-\omega^k}\right)$$

where $\omega$ is a nontrivial fifth root of unity. This is an ‘atomic singular inner function’. To understand what that means, it helps to start with some complex analysis.

The Hardy space $H^\infty$ is the space of bounded analytic functions in the complex unit disk $D$. Any function $f$ in the Hardy space $H^\infty$ can be written as a product of an ‘inner function’ $g$ and an ‘outer function’ $h$:
$$f = gh$$
The inner function $g$ has modulus $1$ almost everywhere on $S^1$. The outer function $h$ has no zeros in $D$ and is completely determined by the boundary values of $|f|$ on the unit circle $S^1$.

The inner function can be further split into two factors, $g=bs$, where $b$ is a ‘Blaschke product’ and $s$ is a so-called ‘singular’ innner function. The Blaschke product is completely determined by the zeros of $f$. The singular inner function is an inner function with no zeros in $D$ and modulus 1 almost everywhere on $S^1$.

So, the singular inner function coming from $f$ is a kind of ‘remainder’ which can neither be determined from the zeros of $f$ in the unit disk nor from $|f|$ on the unit circle!

The prototypical example of a singular inner function is
$$\exp\left(\frac{z+t}{z-t}\right)$$
for any point $t$ on the unit circle. This has an essential singularity at $t$. Starting from this, one gets the most general singular inner function as follows:
$$s(z)=c\,\exp \int_{S^1}\frac{z+t}{z-t}\,d\mu(t)$$
where $\mu$ is a normalized singular measure on $S^1$ and $|c|=1$. Remember, a measure on the circle is singular if it is supported on a set of Lebesgue measure zero. The easiest singular measures to understand are the atomic ones, which are (possibly infinite) linear combinations of Dirac delta measures.

In the example at hand we have taken a linear combination of Dirac deltas supported at the fifth roots of unity. So, the picture uses colors to show the phase $f/|f|$ of the function

$$f(z) = \prod_{k=1}^5 \exp\left(\frac{z+\omega^k}{z-\omega^k}\right)$$

where $\omega=\exp(2\pi i/5)$. This function has essential singularities at the fifth roots of unity, no zeros in $D$, and modulus 1 on $S^1$.

You can learn a lot about a function by looking at a color picture of its phase. For more on this, with lots of wonderful pictures, explore Wegert’s website:

• Elias Wegert, Visualizing complex functions using phase portraits.

and read this paper:

• Elias Wegert, Phase plots of complex functions: a journey in illustration.

The factorization of functions in $H^\infty$ into inner and outer functions is due to Beurling, and it has various generalizations:

• Beurling-Lax theorem, Encyclopedia of Mathematics, Springer.

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!