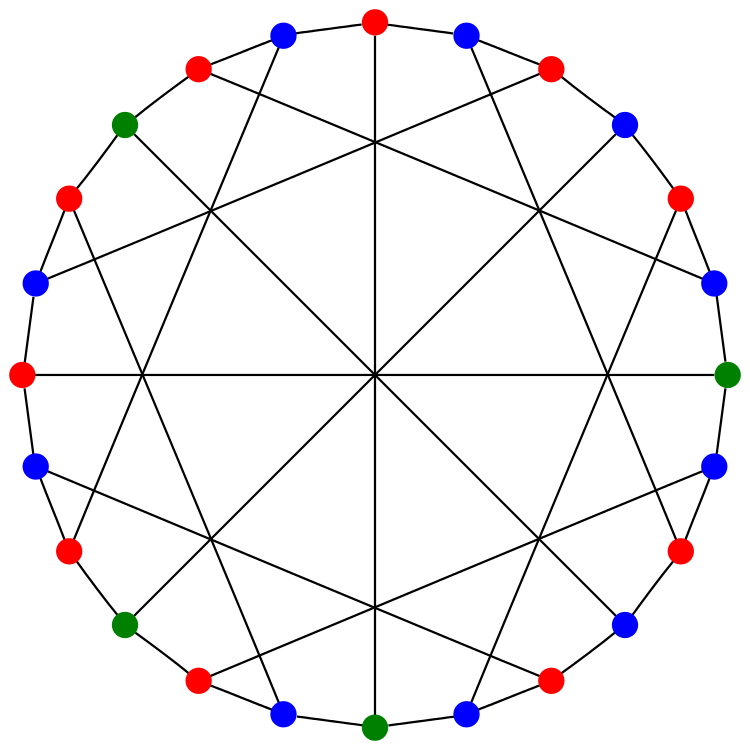
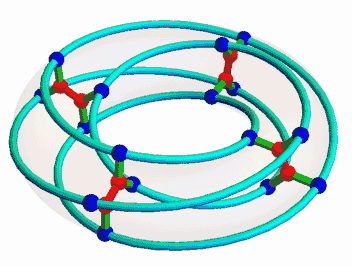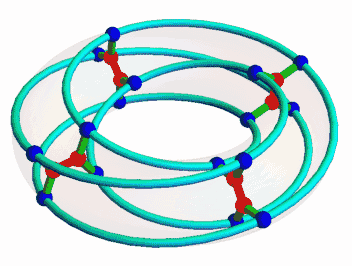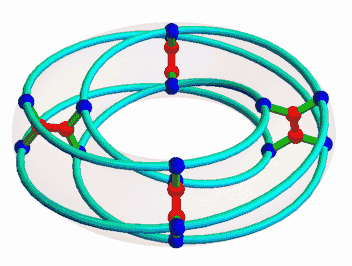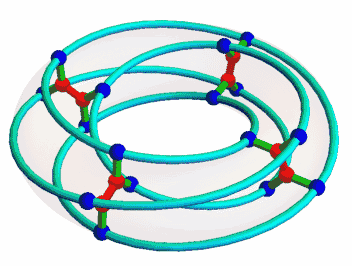
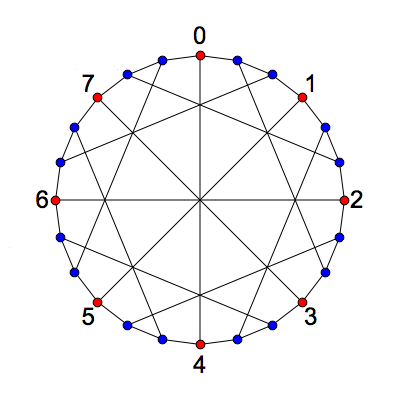
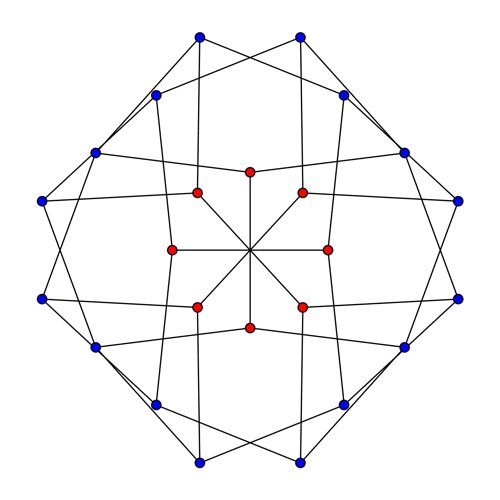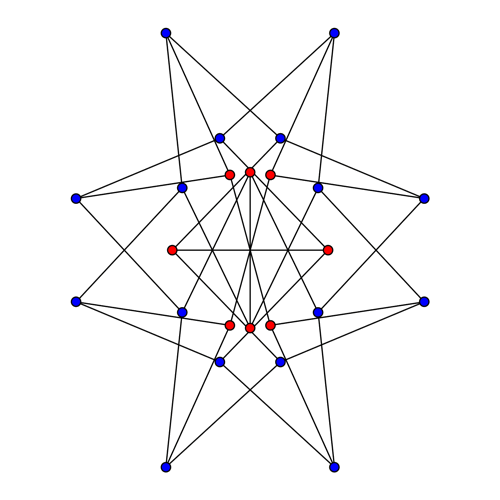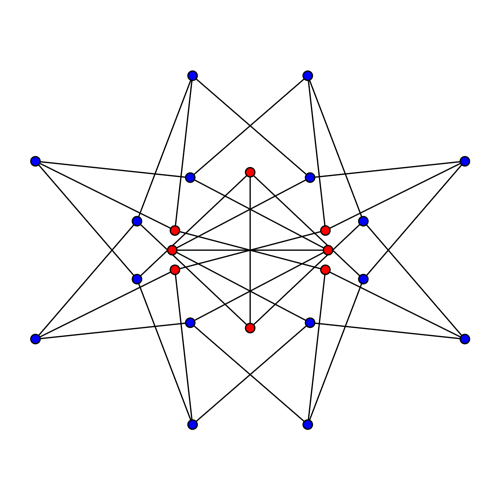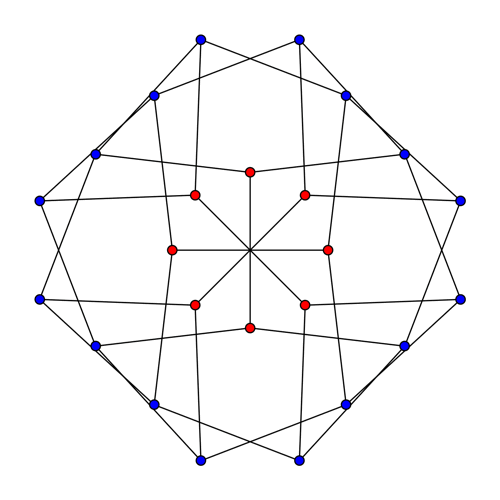
This is the McGee graph. It has 24 vertices and 36 edges. It is a 3-regular graph, meaning that every vertex has 3 neighbors. It also has girth 7, meaning that the shortest cycles have length 7. What makes the McGee graph special is that it has the least number of vertices of any 3-regular graph of girth 7. For this reason we call it a (3,7)-cage.

The McGee graph is the unique (3,7)-cage. It is the smallest (3,\(g\))-cage that is not a Moore graph. It is also the smallest (3,\(g\))-cage whose symmetry group doesn’t act transitively on its vertices: its symmetry group has order 32, and the vertices lie in 2 orbits. This animation by Mamuka Jibladze shows a symmetry of order 8, since the vertices only return to their original positions after two turns:

How does the McGee graph compare to two other cages we have recently seen here, the Heawood graph and Tutte–Coxeter graph?

The Heawood and Tutte–Coxeter graphs are Levi graphs. In other words, they arise from a finite configuration of points and lines, with each vertex corresponding to either a point or line, and an edge connecting two vertices whenever we have a point lying on a line. The McGee graph cannot be a Levi graph, because it is not bipartite. In other words, it doesn’t admit a 2-coloring of its vertices, where the edges only connect vertices of one color to vertices of the other color. The picture above shows a 3-coloring of the McGee graph.

The Heawood and Tutte–Coxeter graphs have symmetry groups that act transitively on their vertices. One reason is that they come from highly symmetrical configurations of points and lines, which even have a ‘duality’ symmetry switching points and lines. In contrast, the symmetry group of the McGee graph does not act transitively on its vertices. Instead, there are two orbits, of size 8 and 16.

Nonetheless, Greg Egan and I were able to describe the McGee graph and its symmetries using ideas from geometry. Our procedure illustrates Klein’s Erlangen program, in which one can ‘reverse-engineer’ a geometry starting from its symmetry group.

The first clue came from a comment by Gordon Royle: the symmetry group of the McGee graph is the group listed as SmallGroup(32,43) in either GAP or Magma. This means that it is the 43rd of the 51 groups of order 32, listed according to a somewhat arbitrary numbering system.

The next step was to understand this group. According to this page:

• Holomorph of \(\mathbb{Z}_8\), GroupProps.

The group SmallGroup(32,43) is the holomorph of the group \(\mathbb{Z}/8\), that is, the semidirect product of \(\mathbb{Z}/8\) with its automorphism group. It is also the general affine group \(\mathrm{GA}(1,\mathbb{Z}/8)\) of the commutative ring \(\mathbb{Z}/8\). This is the group of affine transformations

$$ x \mapsto a x + b , \qquad x \in \mathbb{Z}/8 $$

where \(a,b \in \mathbb{Z}/8\) and \(a\) is invertible.

This suggests describing the vertices of the McGee graph as geometrical figures in the affine line over \(\mathbb{Z}/8\). This is simply \(\mathbb{Z}/8\) regarded not as a ring or group, but as an 8-point set on which affine transformations act as symmetries.

Since the commutative ring \(\mathbb{Z}/8\) is not a field, its affine line has some peculiar features. The only invertible elements are the odd numbers \(1,3,5,7 \in \mathbb{Z}/8\), so only these can play the part of \(a\) in an affine transformation

$$ x \mapsto a x + b $$

Since

$$ 1^2 = 3^2 = 5^2 = 7^2 = 1 \mod 8 $$

the ‘rescaling’ transformations

$$ x \mapsto a x $$

form a copy of Klein 4-group. So, \(\mathrm{GA}(1,\mathbb{Z}/8)\) is the semidirect product of \(\mathbb{Z}/8\), which acts as translations \(x \mapsto x + b\) line, and the Klein 4-group, which acts as rescalings. (Alternatively, we can think of \(\mathrm{GA}(1,\mathbb{Z}/8)\) as the semidirect product of \(\mathbb{Z}/8\) and its automorphism group.)

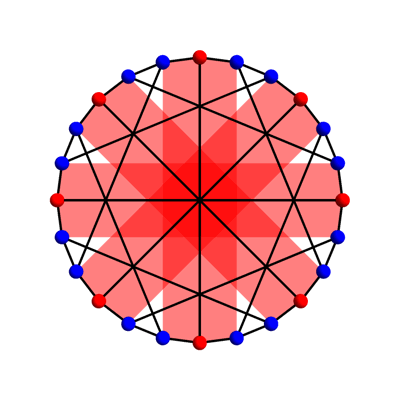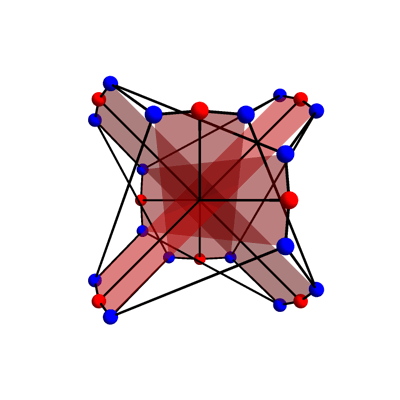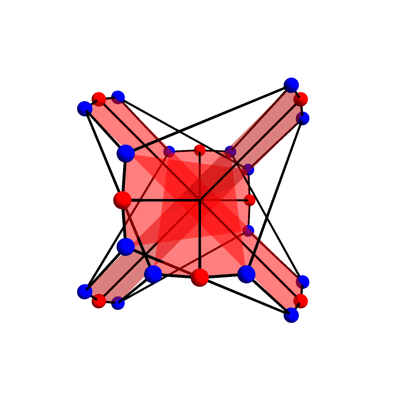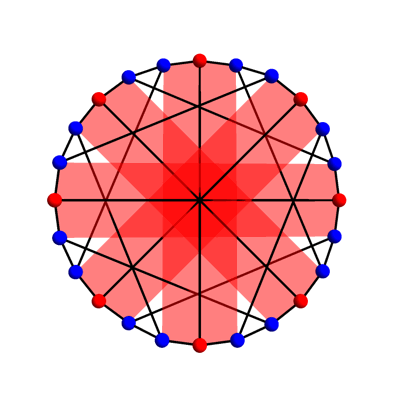
Since the action of \(\mathrm{GA}(1,\mathbb{Z}/8)\) on the McGee graph has two orbits, we will need to use two types of geometrical figure as the vertices of the McGee graph. Since one orbit has size 8, an obvious guess is that 8 vertices should correspond to points of \(\mathbb{Z}_8\). The picture suggests using the 8 red vertices here:

With this choice, two of the 8 red vertices are connected by an edge iff the corresponding points \(x,y \in \mathbb{Z}/8\) are opposite, meaning that

$$ x – y = 4 \mod 8 $$

One should check that the relation of being opposite is preserved by all transformations in \(\mathrm{GA}(1,\mathbb{Z}/8)\). This is clear for translations, and for rescalings it follows from

$$ 3 \cdot 4 = 5 \cdot 4 = 7 \cdot 4 = 4 \mod 8 $$

The translations correspond to rotational symmetries of our picture of the McGee graph. The rescalings correspond to transformations like this:

Note that the 4 red hexagons are set-wise preserved by these transformations. These hexagons correspond to 2 opposite points of \(\mathbb{Z}/8\) and the 4 other vertices of the McGee graph adjacent to these.

It took a few more tries to guess what type of geometrical figure should correspond to the 16 blue vertices of the McGee graph. One clue is that each of blue vertex is adjacent to a single red vertex. Thus, we can define a blue vertex to be a point of \(\mathbb{Z}/8\) together with some extra structure.

Another clue is that each red vertex is adjacent to 2 blue vertices. Thus, whatever this extra structure is, there should be two ways to choose it.

Furthermore, this extra structure must be preserved by affine transformations. In other words, if we have a point equipped with this structure in some way, we can act with an affine transformation on the whole thing, and get another point equipped with a structure of the same sort.

How can we define such a structure?

It helps to find relations between pairs of points in \(\mathbb{Z}/8\) that are invariant under affine transformations. We have already mentioned one. Remember, two points \(x, y \in \mathbb{Z}/8\) are opposite iff

$$ x – y = 4 \mod 8 $$

Here is another: two points are nearby iff

$$ x – y = \pm 2 \mod 8 $$

This relation is clearly invariant under translations; it is invariant under rescalings because

$$ \begin{array}{ccr} 3 \cdot 2 &=& -2 \mod 8 \\
5 \cdot 2 &=& 2 \mod 8 \\
7 \cdot 2 &=& -2 \mod 8 \end{array} $$

And here is a third: we say that two points of \(\mathbb{Z}/8\) are distant iff they are neither nearby nor opposite. This is invariant under affine transformations because the other two relations are. Concretely, two points \(x, y \in \mathbb{Z}/8\) are distant iff their difference is odd:

$$ x – y = 1, 3, 5 \textrm{ or } 7 \mod 8 $$

Beware: don’t take these adjectives too seriously. In the picture of the McGee graph, red vertices that are ‘nearby’ can be farther apart than points that are ‘distant’. Distance in the picture is not preserved by rescalings.

We can use these relations to define geometrical structures on the affine line over \(\mathbb{Z}/8\); these structures will automatically be preserved by affine transformations. The goal is to define a blue vertex in the McGee graph to be a point in the affine line together with some extra structure of this sort.

After our first few attempts failed, Egan figured out how to do it. The key was to define each blue vertex as three red vertices: the red vertex incident to it, and the two other red vertices that can be reached by passing through one other blue vertex. Then, he translated this idea into the affine geometry of \(\mathbb{Z}/8\):

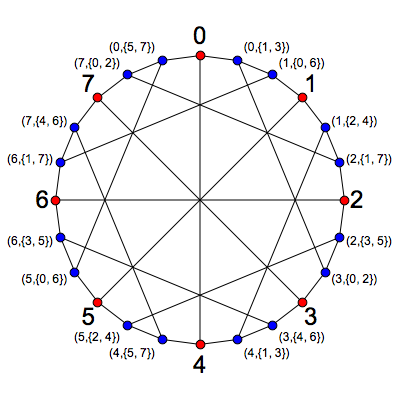
Consider the set \(P\) of ordered pairs \( (p, \{q,r\}) \) where \(p, q, r\) are in \(\mathbb{Z}/8\), \(q\) and \(r\) are nearby (i.e. \(q-r = \pm 2 \mod 8\), and \(p\) is distant to \(q\) and \(r\) (i.e. \(p-q\) and \(p-r\) are odd). To be clear, \( \{q,r\} \) is unordered.

\(P\) contains \(8 \cdot 4 = 32\) ordered pairs, twice the number of blue vertices. But the action on \(P\) of the \(32\) elements of the general affine group is not transitive: there are two 16-element orbits. We pick one of these orbits arbitrarily and use it for the blue vertices of the McGee graph. We then have:

• The red vertices are the 8 elements of \(\mathbb{Z}/8\).

• The blue vertices are ordered pairs from one orbit of \(P\).

• Two red vertices \(p\) and \(p’\) are adjacent when \(p\) and \(p’\) are opposite.

• A red vertex \(p\) and a blue vertex \( (p’, \{q’,r’\})\) are adjacent when \(p = p’\).

• Two blue vertices \((p, \{q,r\})\) and \((p’, \{q’,r’\})\) are adjacent when \(p \in \{q’,r’\}\) and \(p’ \in \{q,r\}\).

So we’ve ended up defining each blue vertex as three red vertices: the blue vertex’s direct neighbour, and the two other red vertices that can be reached by passing through one other blue vertex.

This picture shows how it works:

The tricky part is choosing 16 of the 32 elements of \(P\), one orbit of the general affine group, to be the blue vertices of our McGee graph. There must be something invariant under the affine group that picks out \( (p, \{q,r\})\) as belonging to one orbit or the other. But what?

Egan answered this too:

Here’s a simple linear invariant for distinguishing the orbits.

$$ f(p,\{q,r\}) = q + r – 2p $$

\(f\) is \(0\) on one orbit and \(4\) on the other. For example,

$$ f(0,\{1,7\}) = 1 + 7 – 2 \cdot 0 = 0 $$

$$ f(0,\{1,3\}) = 1 + 3 – 2 \cdot 0 = 4 $$

To see that \(f\) is invariant, first note that it can only take values from \(\{0,4\}\).

If \(p\) is even, then \(2p\) is divisible by 4. But if \(p\) is even, \(q\) and \(r\) are both odd numbers separated by \(2\), and \(q+r = 1+3, 3+5, 5+7,\) or \(7+1\), which are all divisible by \(4\).

If \(p\) is odd, then \(2p = 2 \mod 4\), but \(q\) and \(r\) are both even numbers separated by \(2\), and \(q+r = 0+2, 2+4, 4+6\) or \(6+0\), which are all equal to \(2 \mod 4\). So either way, \(q + r – 2p = 0 \mod 4\).

Now, we have:

$$ f(ap+b, \{aq+b, ar+b\}) = a (q+r-2p) = a f(p,\{q,r\}) $$

But multiplication of \(0\) or \(4\) by any of the invertible elements \(1, 3, 5\) or \(7\) gives you back the original result.

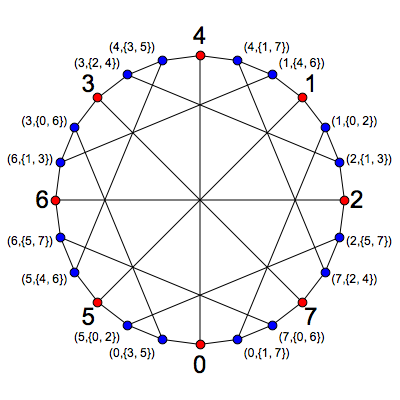
If we choose the other orbit of \(P\) to be the blue vertices of our graph, we get this:

At first this looks different from the graph we have seen, but drawing it another way reveals it to be a copy of the McGee graph:

Egan also found a nice explanation for why this works:

The function

$$ T: \mathbb{Z}/8 \to \mathbb{Z}/8 $$

with

$$ T(x) = x + 2 (x \;\mathrm{mod}\; 2) $$

adds 2 to the odd numbers only. Although this is clearly not an element of \(\mathrm{GA}(1,\mathbb{Z}/8)\), it preserves the relationships ‘opposite’, ‘nearby’ and ‘distant’, so it acts on \(P\). And it swaps the values \(0\) and \(4\) of the invariant \(f(p,\{q,r\}) = q + r – 2p\):

$$ f(T(p),\{T(q),T(r)\}) = f(p,\{q,r\}) \pm 4 $$

So \(T\) maps each orbit of \(\mathrm{GA}(1,\mathbb{Z}/8)\) on \(P\) into the other orbit, and gives a graph isomorphism between the two versions of the McGee graph with blue vertices taken from the two orbits.

Mapping the McGee graph into the plane

On a different note, Ed Pegg Jr. has found a way to map the McGee graph into the plane so that all edges have unit length:

He asked if this embedding is rigid: in other words, if it is impossible to slightly move the vertices in a nontrivial way while each edge maintains the same length. Here Euclidean transformations, meaning composites of translations and rotations, count as trivial.

A necessary but not sufficient condition for rigidity is ‘infinitesimal rigidity’. A map from a graph into the plane is infinitesimally rigid if the only infinitesimal changes in the positions of the vertices leaving all edge lengths unchanged to first order are those arising from Euclidean transformations. If it is not infinitesimally rigid, we say the map is infinitesimally flexible.

Infinitesimal rigidity can be determined by examining a system of linear equations with one variable for each coordinate of each vertex and one equation for each edge. Using a computer calculation, Greg Egan showed that for the above embedding of the McGee graph this system of equations has a 12-dimensional space of solutions. This is just what one would naively expect due to the McGee graph having 24 vertices and 36 edges:

$$ 2 \times 24 \; – \; 36 = 12. $$

Thus, there are no linear dependencies between the 36 equations. When we take the 12-dimensional space of solutions and mod out by the 3-dimensional space of infinitesimal Euclidean transformations, we are left with a 9-dimensional space.

In short, the McGee graph is infinitesimally flexible, with 9 degrees of freedom. It is therefore natural to conjecture that the McGee graph is not rigid. Egan went on to prove that it is not, and illustrated this fact here:

For more details, see:

• Ed Pegg Jr., Is unit McGee rigid?, Mathematics Stack Exchange, October 17, 2015.

Credits

The featured image at the top of this post was made by Koko90 and placed on Wikicommons under a Creative Commons Attribution-Share Alike 3.0 Unported license.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!