This image by Greg Egan shows 5 ways to inscribe a regular tetrahedron in a regular dodecahedron. More precisely, it shows 5 ways to choose 4 vertices of the dodecahedron that are also vertices of a regular tetrahedron.

The union of all these tetrahedra is a nonconvex polyhedron called the compound of 5 tetrahedra, first described by Edmund Hess in 1876.

This polyhedron is chiral: it has no reflection symmetries. In rough terms, it has an inherent ‘left-handedness’: if you start at a point where the 5 tetrahedra meet, you’ll see the lines of intersection ‘swirl counterclockwise’ as they go out.

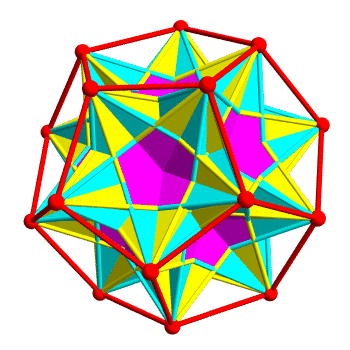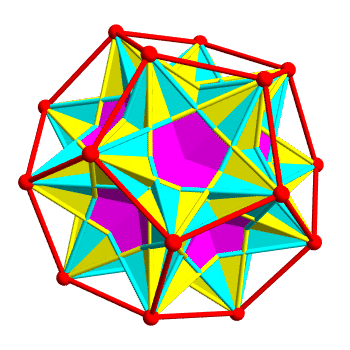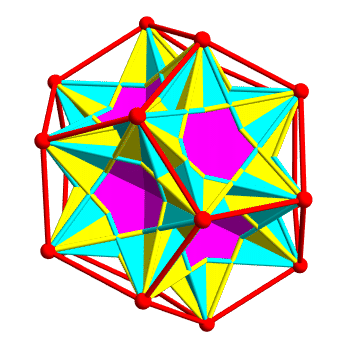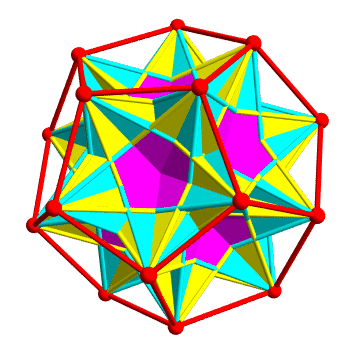
In fact there are 10 ways to inscribe a regular tetrahedron in a regular dodecahedron. 5 form the left-handed polyhedron above, and the other 5 give the right-handed version of this polyhedron. The union of all 10 tetrahedra is a polytope called compound of 10 tetrahedra, which has reflection symmetries:

The two kinds of tetrahedra are colored yellow and cyan. Regions belonging to both are colored magenta. It’s pretty—but it’s hard to see the individual tetrahedra, because they overlap a lot.

We can do something similar starting with a cube:

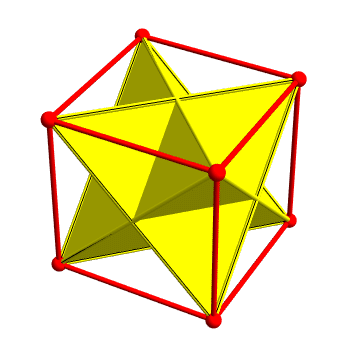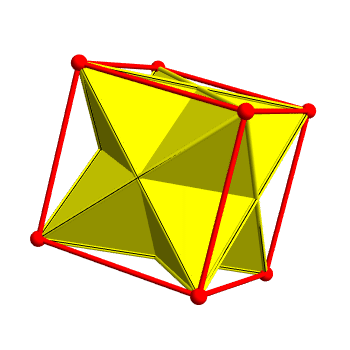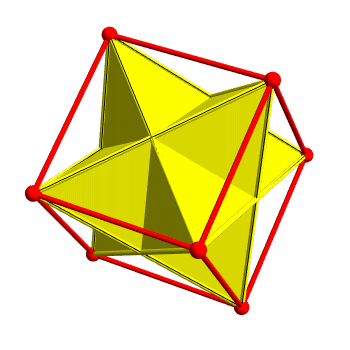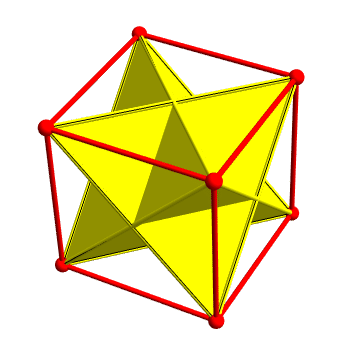
There are 2 ways to inscribe a regular tetrahedron in a cube. Taken together they form a nonconvex polyhedron called the stellated octahedron.

There are 5 ways to inscribe a cube in a dodecahedron. Their union is called the compound of 5 cubes:

Inscribing 2 tetrahedra in each of these cubes, we obtain the 10 tetrahedra in the dodecahedron.

What is the mathematics underlying these relationships between the tetrahedron, cube and dodecahedron? The finite subgroups of the rotation group $\mathrm{SO}(3)$ can be classified, up to conjugation:

• for each $n \ge 1$, the cyclic group $\mathbb{Z}/n$,

• for each $n \ge 2$, the dihedral group $\mathrm{D}_n$,

• the rotational symmetry group of the tetrahedron, which is isomorphic to the alternating group $\mathrm{A}_4$, the group of even permutations of the tetrahedron’s 4 vertices.

• the rotational symmetry group of the cube, which is isomorphic to the symmetric group $\mathrm{S}_4$, the group of permutations of the cube’s 4 diagonal axes.

• the rotational symmetry group of the dodecahedron, which is isomorphic to the symmetric group $\mathrm{A}_5$, the group of even permutations of the 5 cubes inscribed in the dodecahedron.

So, what’s at work here is a relation between $\mathrm{A}_4, \mathrm{S}_4$ and $\mathrm{A}_5$, both as abstract groups and as subgroups of $\mathrm{SO}(3)$.

• Tetrahedron and cube. $\mathrm{A}_4$ is a subgroup of $\mathrm{S}_4$. So, every symmetry of an inscribed tetrahedron gives a symmetry of the cube. Since $\mathrm{A}_4$ is a subgroup of $\mathrm{S}_4$ in a unique way, both tetrahedra in the cube have the same subgroup of $\mathrm{S}_4$ as symmetries—not merely conjugate subgroups.

• Tetrahedron and dodecahedron. $\mathrm{A}_4$ is a subgroup of $\mathrm{A}_5$. So, every symmetry of an inscribed tetrahedron gives a symmetry of the dodecahedron. $\mathrm{A}_4$ is a subgroup of $\mathrm{A}_5$ in 5 different ways that are all conjugate. For each of these 5 subgroups, 2 of the 10 tetrahedra in the dodecahedron have this subgroup as symmetries.

• Cube and dodecahedron. $\mathrm{S}_4$ is not a subgroup of $\mathrm{A}_5$. So, not every symmetry of an inscribed cube gives a symmetry of the dodecahedron.

Puzzle 1: Describe a tetrahedron in a cube, tetrahedron in a dodecahedron or cube in a dodecahedron using the language of group theory. Use this to explain why there are 2 tetrahedra in the cube, 10 tetrahedra in the dodecahedron and 5 cubes in the dodecahedron.

Puzzle 2: $\mathrm{A}_4$ is a normal subgroup of $\mathrm{S}_4$ but not of $\mathrm{A}_5$. How does this make tetrahedra in the cube different than tetrahedra in the dodecahedron?

For more, see:

• Alternating group $\mathrm{A}_4$, Groupprops.

• Symmetric group $\mathrm{S}_4$, Groupprops.

• Alternating group $\mathrm{A}_5$, Groupprops.

• Classification of finite subgroups of $\mathrm{SO}(3)$, Groupprops.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!