Here Greg Egan has drawn two regular dodecahedra, in red and blue. They share 8 corners—and these are the corners of a cube, shown in green.

Note that not every symmetry of the cube is a symmetry of either dodecahedron it is inscribed in. If you give the cube a 90° rotation around any face, the red and blue dodecahedra are not mapped to themselves: they are interchanged. Following Adrian Ocneanu, let us call these twin dodecahedra.

But there are actually 5 different ways to take a regular dodecahedron and make them into the corners of a cube, as shown here:

Each one gives the dodecahedron a different twin! So, despite the connotations of the word ‘twin’, a dodecahedron actually has 5 twins.

But here’s something deeper that Ocneanu claims to have proved, in unpublished work. Suppose you take one of these twins. It, too, will have 5 twins. One of these will be the dodecahedron you started with. But the other 4 will be new dodecahedra: that is, dodecahedra rotated in new ways.

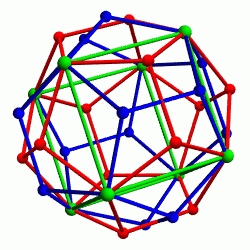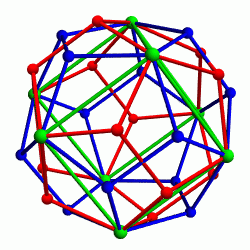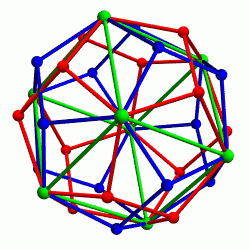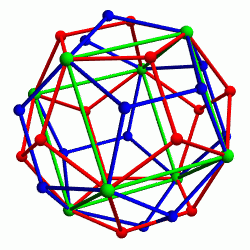
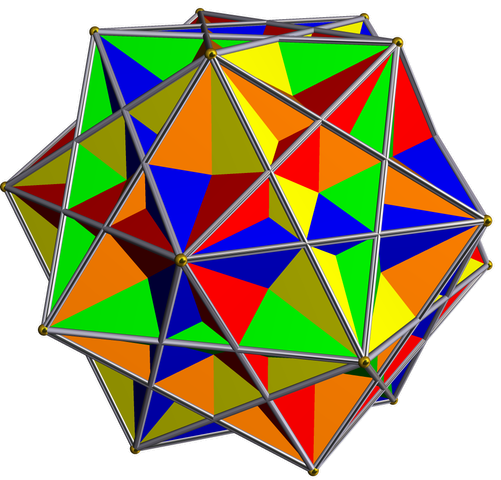
How many different dodecahedra can you get by continuing to take twins? Infinitely many! This image by Roice Nelson shows the vertices of a dodecahedron, its twins, the twins of its twins, the twins of the twins of its twins, the twins of the twins of the twins of its twins, and the twins of the twins of the twins of the twins of its twins:

All these vertices are shown in a stereographic projection.

In fact, we can create a graph that explains the situation. Start with a node for our original dodecahedron. Draw nodes for all the dodecahedra you can get from this one by repeatedly taking twins. Connect two nodes with an edge if and only if they are twins of each other.

Ocneanu claims the resulting graph is a tree! In other words, if you start at your original dodecahedron, and keep walking along edges of this graph by taking twins, you’ll never get back to where you started except by undoing all your steps.

Greg Egan and I have been trying to check this using ideas from a conversation I had with Ocneanu. Here’s where we’ve gotten so far.

Start with a 4-simplex whose 5 vertices are unit quaternions. Call the vertices

$$ q_0, q_1, q_2, q_3, q_4 $$

Form the 25 ratios \( q_i q_j^{-1} \). Five of these equal 1. The remaining 20, namely those with \(i \ne j\), lie on a 3-dimensional hyperplane in the quaternions. And in fact, these are the 20 vertices of a regular dodecahedron!

Egan has checked this by direct calculation, but here is another way, which while roundabout is quite interesting. The rotational symmetries of the 4-simplex form a 60-element subgroup

$$ G \subseteq \mathrm{SO}(4). $$

This is isomorphic to the group of even permutations of the vertices of the 4-simplex, namely \(\mathrm{A}_5\).

Left and right multiplications by unit quaternions act as rotations in 4 dimensions, and the group of unit quaternions is isomorphic to \(\mathrm{SU}(2)\). This can be used to exhibit \(\mathrm{SU}(2) \times \mathrm{SU}(2)\) as the double cover of \(\mathrm{SO}(4)\): a pair of unit quaternions \((g,h)\) acts as a rotation of the space of quaternions by

$$ q \mapsto g q h^{-1} , $$

but \((g,h)\) and \((-g,-h)\) act as the same rotation.

Thus, sitting over \(G\) we obtain a 120-element group

$$ \widetilde{G} \subset \mathrm{SU}(2) \times \mathrm{SU}(2) $$

where the tilde simply means this group is a double cover of \(G\). We can then map \(\widetilde{G}\) down to \(\mathrm{SU}(2)\) and get a subgroup of the unit quaternions. We can actually do this in two ways, projecting down to the left or right factor of \(\mathrm{SU}(2) \times \mathrm{SU}(2)\) via

$$ p_L, p_R : \mathrm{SU}(2) \times \mathrm{SU}(2) \to \mathrm{SU}(2) . $$

Are the resulting subgroups

$$ G_L = p_L\widetilde{G}, \quad G_R = p_R\widetilde{G} $$

isomorphic? How many elements do they have? What do they look like? We can show they’re isomorphic, and also isomorphic to \(\widetilde{G}\). Each one has 120 elements, forming the vertices of a 600-cell in the unit quaternions!

To check this, it helps a lot to know that there aren’t many finite subgroups of \(\mathrm{SU}(2)\) except for cyclic and dihedral groups. Up to isomorphism, there are just three:

• the binary tetrahedral group: the subgroup of \(\mathrm{SU}(2)\) double covering the rotational symmetry group of the tetrahedron, which has 24 elements, forming the vertices of the 24-cell,

• the binary octahedral group: the subgroup of \(\mathrm{SU}(2)\) double covering the rotational symmetry group of the octahedron or cube, which has 48 elements, forming the vertices of two dual 24-cells, and

• the binary icosahedral group: the subgroup of \(\mathrm{SU}(2)\) double covering the rotational symmetry group of the icosahedron or dodecahedron, which has 120 elements, forming the vertices of a 600-cell.

The group \(\widetilde{G}\) is a 120-element group that maps onto \(A_5\). The only groups with this property are \(A_5 \times \mathbb{Z}/2\) and the binary icosahedral group. These are the two central extensions of \(\mathrm{A}_5\) by \(\mathbb{Z}/2\).

In either case, the options for what we get when we map \(\widetilde{G}\) down to get a subgroup of the left or right copy of \(\mathrm{SU}(2)\) are severely limited. Since \(\mathrm{A}_5\) is a simple group, the only possible quotient groups of either \(\mathrm{A}_5 \times \mathbb{Z}/2\) or the binary icosahedral group are these groups themselves, \(\mathrm{A}_5\), \(\mathbb{Z}/2\) or the trivial group.

\(\mathrm{A}_5 \times \mathbb{Z}/2\) and \(\mathrm{A}_5\) just can’t show up as finite subgroups of \(\mathrm{SU}(2)\): they’re not on the list. So, the only options for we get when we map \(\widetilde{G}\) down to either the left or right \(\mathrm{SU}(2)\) are the binary icosahedral group, \(\mathrm{Z}_2\) or the trivial group. But it’s easy to see that we get a group with more than two elements. So, we must get the binary icosahedral group.

In short, \(G_L\) and \(G_R\) are both copies of the binary icosahedral group in the unit quaternions. You can think of either one as the vertices of a 600-cell.

Furthermore, since \(G_L\) and \(G_R\) have 120 elements just like \(\widetilde{G}\) itself, the maps

$$ p_L : \widetilde{G} \to G_L, \qquad p_L : \widetilde{G} \to G_L $$

are isomorphisms. So, \( \widetilde{G} \) is the binary icosahedral group. Moreover, if we write \(g_L\) for \(p_Lg\) and \(g_R\) for \(p_Rg\), we must have

$$ \widetilde{G} = \{(g_L , g_R) : g \in \widetilde{G} \} . $$

Given how pairs of unit quaternions act as rotations of the quaternions, any element \(g \in \widetilde{G}\) acts to permute the vertices \(q_i\) of the 4-simplex via

$$ q_i \mapsto g_L \, q_i \, {g_{R}}^{-1} . $$

Let’s use this to see why the 20 points

$$ \{ q_i q_j^{-1} :\; 0 \le i, j \le 4 , \; i \ne j \} $$

form the vertices of a dodecahedron. First, note that from the geometry of a 4-simplex, we have:

$$ q_i \cdot q_j = -\frac{1}{4} $$

for all \(i \ne j \). In terms of quaternion operations this says

$$ \mathrm{Re}(q_i {q_j}^*) = \mathrm{Re}(q_i q_j^{-1}) = -\frac{1}{4} . $$

So, all 20 points lie on a 3-dimensional hyperplane in the quaternions, where the real part takes a constant value.

Second, any \(g \in \widetilde{G}\) acts to permute the vertices \(q_i\) and thus the 20 points \(q_i^{-1} q_j\) where \(i \ne j\). Since this group is the binary icosahedral group, since it is acting on these points by rotations of 3d space, in fact as symmetries of a dodecahedron, and since it is acting transitively on these 20 points, the only possibility is that these points are the vertices of a dodecahedron.

Now, following Egan, let us build the ‘tree of twins’ of this dodecahedron. We start by building the first 5 twins. Let us call the vertices of our dodecahedron

$$ D^0_{i,j} = q_i q_j^{-1} , \qquad i \ne j . $$

For \( m = 0,1,2,3,4\) we build a new set of 20 points

$$ D^{1,m}_{i,j} = q_m^{-1} q_j^{-1} q_i q_m, \qquad i \ne j .$$

We can check that for each \(m\) these, too, are the vertices of a dodecahedron. After all, the argument that the points \(q_i q_j^{-1}\) with \(i \ne j\) lie on the hyperplane of quaternions with real part \(-1/4\) works equally well for the points \(q_j^{-1} q_i\), and conjugating by \(q_m\) maps this hyperplane to itself, just rotating these points.

Now, fix \(m\), and let \(i \ne j \) range from \(1\) to \(5\). We can check that the intersection of the 20 points \(D^{1,m}_{i,j}\) and the original set of 20 points \(D^{0,m}_{i,j}\) consists of the 4 points

$$ D^{1,m}_{m,j} = q_m^{-1} \, q_j \, q_m^{-1} \, q_m = q_m^{-1} q_j = D^0_{m,j} \qquad j \ne m $$

together with the 4 points

$$ D^{1,m}_{i,m} = q_m^{-1} \, q_m \, q_i^{-1} \, q_m = q_i^{-1} q_m = D^0_{i,m} \qquad i \ne m .$$

It is clear that each of these sets of 4 points are the vertices of a regular tetrahedron, obtained by applying some isometry to the 3-face of the 4-simplex that excludes \(q_m\). And these two tetrahedra are mapped into each other by quaternionic conjugation, which is the same as them being mapped into each other by negation in \(\mathbb{R}^3\) if we identify \( \mathbb{R}^3\) with the hyperplane of quaternions with real part \(-1/4\). So together they make a cube.

So, we have seen that as \(m\) ranges from \(1\) to \(5\), each set \(D^{1,m}_{i,j}\) is the set of vertices of a dodecahedron that is one the 5 twins of \(D^{0,m}_{i,j} \).

We can now construct the whole tree of twins, twins-of-twins, twins-of-twins-of-twins, and so on as follows. For the \(N\)th level in the tree, we label each dodecahedron with a sequence \(m_1, m_2, m_3, \dots, m_N \) where each \(m_k\) ranges from \(0\) to \(4\), and \(m_k \ne m_{k+1} \).

When \(N\) is even, the vertices of the dodecahedron are:

$$ D^{N,m_1,\, \dots\, ,m_N}_{i,j}
= q_{m_1} \, q_{m_2}^{-1} \, \cdots \, q_{m_N}^{-1} \, q_i q_j^{-1} \, q_{m_N} \, \cdots \, q_{m_2} \, q_{m_1}^{-1} $$

When \(N\) is odd, the vertices are:

$$ D^{N,m_1,\, \dots\, , m_N}_{i,j}
= q_{m_1} \, q_{m_2}^{-1} \, \cdots q_{m_N} \, q_j^{-1} q_i q_{m_N}^{-1} \, \cdots \, q_{m_2} \, q_{m_1}^{-1} $$

The whole \((2N+2)\)-fold product always has an inverse for every second term; this determines whether we have \(q_i q_j^{-1}\) in the middle, or \( q_j^{-1} q_i\).

To see that successive entries in the tree really are twins, first suppose that \(N\) is even, and we add a new index \(p \ne m_N\) to the sequence to get an odd-level dodecahedron. Then, for \(r \ne p\):

$$ D^{N+1,m_1,\, \dots\, , m_N,p}_{p,r}
= q_{m_1} \, q_{m_2}^{-1} \, \cdots \, q_{p} \, q_r^{-1} \, q_p q_p^{-1} \, \cdots \, q_{m_2} \, q_{m_1}^{-1}
= D^{N,m_1,\, \dots\, , m_N}_{p,r} $$

and

$$ D^{N+1,m_1,\, \dots\, , m_N,p}_{r,p}
= q_{m_1} \, q_{m_2}^{-1} \, \cdots \, q_p \, q_p^{-1} \, q_r q_p^{-1}\, \cdots \, q_{m_2} \, q_{m_1}^{-1}
= D^{N,m_1,\, \dots \,, m_N}_{r,p} $$

So \(D^{N+1,m_1,\,\dots\, , m_N,p}\) and \(D^{N,m_1,\,\dots\, , m_N}\) share 8 vertices, making them twins.

Next, suppose that \(N\) is odd, and we add a new index \(p \ne m_N\) to the sequence to get an even-level dodecahedron. Then, for \(r \ne p\):

$$ D^{N+1,m_1,\, \dots\, , m_N,p}_{p,r}
= q_{m_1} \, q_{m_2}^{-1}\, \cdots \, q_p^{-1} \, q_p \, q_r^{-1} \, q_p \, \cdots \, q_{m_2} \.\, q_{m_1}^{-1}
= D^{N,m_1,\, \dots\, , m_N}_{p,r} $$

and

$$ D^{N+1,m_1,\, \dots\, , m_N,p}_{r,p}
= q_{m_1} \, q_{m_2}^{-1} \, \cdots \, q_p^{-1} \, q_r \, q_p^{-1} \, q_p \, \cdots \, q_{m_2} \, q_{m_1}^{-1}
= D^{N,m_1,\, \dots\, , m_N}_{r,p} $$

So again we have 8 vertices in common between \(D^{N,m_1,\,\dots\,, m_N,p}\) and \(D^{N,m_1,\,\dots\, , m_N}\).

We have thus constructed the tree of twins of a dodecahedron! However, Ocneanu’s deeper claim is that each dodecahedron in this tree is distinct. This is what gives a tree where each node is a distinct dodecahedron formed by repeatedly taking twins of our original dodecahedron, and two nodes are connected by an edge if and only if they are twins of each other.

Ocneanu told me that the key is to first prove a result about the 4-simplex. I have not done it, so I leave it as a puzzle:

Puzzle 1: Can you prove that if we take a regular 4-simplex whose vertices \(q_0, q_1, q_2, q_3, q_4\) are unit quaternions with \(q_0 = 1\), the other vertices generate a free group on 4 elements?

You can find a proof here, though I’m still hoping for a simpler one:

• John Baez, Do unit quaternions at vertices of a regular 4-simplex, one being 1, generate a free group?, MathOverflow.

Using this, Egan and I proved that all the dodecahedra in the tree of twins are distinct. Here’s how:

Proof. First, it suffices to prove that no other dodecahedron in the tree equals the original dodecahedron \(D^0\), i.e. the root of the tree, since while we have described the tree as a rooted tree, the root is purely conventional.

Second, it suffices to assume \(q_0 = 1\), since rotating the 4-simplex merely has the effect of rotating all dodecahedra in the tree of twins in unison.

Fix \(N \gt 0\). We want to prove that we cannot get a set of vertices \(D^{N,m_1,\, \dots\, ,m_N}_{i,j}\) that equals the set of vertices of the original dodecahedron, namely

$$ D^0_{i,j} = q_i q_j^{-1} $$

Recall that we always have \(i \ne j\) and \(m_k \ne m_{k+1}\).

First consider the case where \(N\) is even. We have

$$ D^{N,m_1,…m_N}_{i,j} = g \, q_i \, q_j^{-1} \, g^{-1} $$

where

$$ g = q_{m_1} \, q_{m_2}^{-1} \, \cdots \, q_{m_N}^{-1} $$

We need to prove that the set of dodecahedron vertices \( q_i q_j^{-1} \) cannot equal the set of dodecahedron vertices \( g q_i q_j^{-1} g^{-1}\). In other words, we need to prove that \(g\) cannot act as a rotational symmetry of the dodecahedron \(q_i q_j^{-1}\).

For this, it is necessary and sufficient to show that any expression of the form

$$ g = q_{m_1} \, q_{m_2}^{-1} \, \cdots \, q_{m_N}^{-1} $$

cannot equal the identity if \(N \gt 0\) and \(m_k \ne m_{k+1}\) for all \(k\). After all, if we had \(g = 1\) then \(g\) would be a rotational symmetry of the dodecahedron. Conversely, if \(g\) were a rotational symmetry of the dodecahedron, some power of it would equal \(1\). But since we’re assuming \(g\) is an element of a free group, this would imply that \(g = 1\).

It is easy to see that an expression \(g\) of the above form cannot equal 1. We have \(q_0 = 1\), but \(m_k \ne m_{k+1}\), so at most every other term in the product

$$ q_{m_1} \, q_{m_2}^{-1} \, \cdots \, q_{m_N}^{-1} $$

can equal 1. This does not allow for a cancellation of all the factors, given our assumption that \(q_1, q_2, q_3, q_4\) generate a free group. Removing each \(q_0\) from the product will just bring two inverses or two non-inverses together that were previously separated, so there won’t be any further cancellation, and it is impossible for the whole product to be reduced to 1.

Next consider the case where \(N\) is odd. Suppose some dodecahedron \(D^{N,m_1,…,m_N}\), which we’ll abbreviate as \(D^{\mathrm{odd}}\), has the same set of vertices as \(D^0\). As before, define

$$ g = q_{m_1} \, q_{m_2}^{-1} \, \cdots \, q_{m_{N-1}}^{-1} $$

Also, define:

$$ D^{\mathrm{even}}_{i,j} = g D^0_{i,j} g^{-1} $$

\(D^{\mathrm{even}}\) is the predecessor of \(D^{\mathrm{odd}}\) in the tree of twins, and hence one of its twins. We know from the construction of the tree that \(D^{\mathrm{even}}\) and \(D^{\mathrm{odd}}\) have the following vertices in common:

$$ D^{\mathrm{odd}}_{m_N,j} = D^{\mathrm{even}}_{m_N,j} $$

for \(j \ne m_N\). Let’s choose a particular such \(j\). We are assuming \(D^{\mathrm{odd}} = D^0\), so this is saying that there exist indices \(a \ne b\) such that:

$$ D^0_{a,b} = g D^0_{m_N,j} g^{-1} $$

or in other words:

$$ q_a q_b^{-1} = g \, q_{m_N} \, q_j^{-1} \, g^{-1} $$

so that

$$ q_a^{-1} \, g \, q_{m_N} \, q_j^{-1} \, g^{-1}\, q_b = 1 $$

We have \( j\ne m_N\), and since there are four possibilities we can also choose \(j \ne m_{N-1}\). Thus, \(q_j^{-1}\) will not cancel with either the \(q_{m_N}\) before it or the \(q_{m_{N-1}}\) that is the first term of \(g^{-1}\). Nor will \(q_{m_N}\) cancel with the last term of \(g\), which is \(q_{m_{N-1}}^{-1}\).

It is possible that either \(a = m_1\) or \(b = m_1\), in which case terms will cancel at the beginning or end, but at most we lose two terms from the product. So we have a product that still contains at least two terms, consisting of alternating inverses and non-inverses of the \(q_i\), with no successive indices equal. As noted before, products like this can never equal \(1\) given our assumption that \(q_1, \dots, q_4\) generate a free group, even when we allow any number of non-successive terms to be \(q_0 = 1\). So, we obtain a contradiction.   █

We conclude with some more puzzles due to Egan:

Puzzle 2: Prove that the rotational symmetry groups of the dodecahedra with vertices:

$$ q_i q_j^{-1} , \qquad i \ne j $$

and

$$ q_i^{-1} q_j , \qquad i \ne j $$

are precisely the subgroups of \(\mathrm{SO}(3)\) covered by the groups \(G_L, G_R \subset \mathrm{SU}(2) \) defined above, if we let \(g \in \mathrm{SU}(2)\) act as rotations of the hyperplane \(\mathrm{Re}(q) = -1/4\) via \( x \mapsto g x g^{-1} \).

Puzzle 3: Show that these points are the vertices of a 4-simplex:

$$ q_0 = 1 $$

$$q_1 = -\frac{1}{4} + \frac{\sqrt{5}}{4} i + \frac{\sqrt{5}}{4} j + \frac{\sqrt{5}}{4} k $$

$$ q_2 = -\frac{1}{4} + \frac{\sqrt{5}}{4} i -\frac{\sqrt{5}}{4} j -\frac{\sqrt{5}}{4} k $$

$$ q_3 = -\frac{1}{4} -\frac{\sqrt{5}}{4} i + \frac{\sqrt{5}}{4} j -\frac{\sqrt{5}}{4} k $$

$$ q_4 = -\frac{1}{4} -\frac{\sqrt{5}}{4} i -\frac{\sqrt{5}}{4} j +\frac{\sqrt{5}}{4} k $$

Show that with this choice, the vertices of every dodecahedron in the tree of twins lies in the golden field \(\mathbb{Q}[\sqrt{5}]\). Each vertex will be a unit quaternion, but because it will have \(\mathrm{Re}(q)=-1/4\), as a point in \(\mathbb{R}^3\) it will have squared norm \(15/16\).

Puzzle 4: Prove the following simple recursive formula for the tree of twins. For even \(N\):

$$ D^{N+1,m_1,…m_N,p}_{i,j} = D^{N,m_1,…m_N}_{p,j} D^{N,m_1,…m_N}_{i,p} $$

For odd \(N\):

$$ D^{N+1,m_1,…m_N,p}_{i,j} = D^{N,m_1,…m_N}_{i,p} D^{N,m_1,…m_N}_{p,j}$$

Puzzle 5: Take a cube with axes

$$A = \{ (1,0,0), (0,1,0), (0,0,1)\} .$$

Prove that there is an order-5 rotation \(R\) that you can apply 1, 2, 3 or 4 times to \(A\) to give you the axes of the other 4 cubes associated with one of the dodecahedra containing the original cube.

Prove that there is another order-5 rotation, \(S\), that similarly gives you the cubes associated with the other dodecahedron containing the original cube.

We can treat each edge in the tree of twins as a cube: the cube in common to the dodecahedra connected by that edge. Prove that you can traverse the whole tree, visiting every edge, by constructing cubes whose axes are the column vectors of the following rotation matrices:

$$ I, \; R^k , \, \; S^k , \; R^k S^\ell , \; S^k R^\ell , \; R^k S^\ell R^m , \; S^k R^\ell S^m , \dots $$

etcetera, where the powers \(k, \ell, m, \dots\) range from 1 to 4.

These column vectors are all unit vectors whose components lie in the golden field \(\mathbb{Q}[\sqrt{5}]\). If you take all three column vectors from each matrix, along with their negations, you get 6 vectors per matrix:

• Level 0: 6 vectors from the identity matrix \(I\),
• Level 1: 48 vectors from \(R^k, S^k\),
• Level 2: 192 vectors from \(S^k R^\ell, R^k S^\ell\),

and in general \(6 \cdot 2 \cdot 4^N\) vectors from level \(N\), except for \(N=0\), when we get 6.

Prove that the vectors from levels \(1\) through \(N\) consist of precisely one copy of every unit vector whose components can be written as:

$$ \frac{i + j \sqrt{5}}{2^{N+1}} $$

for integers \(i\) and \(j\). In other words this process generates, without repetitions, all unit vectors of this form.

Since this last puzzle is quite interesting but also apparently rather hard, we present Egan’s solution below. His solution uses a computer to do some lengthy calculations. Can you find a shorter, more conceptual proof?

In his solution, Egan describes not which vectors show up in levels \(1\) through \(N\), but which vectors show up at exactly the \(N\)nth level:

Theorem. Suppose we start with a cube whose axes are aligned with the standard basis for \(\mathbb{R}^3\). There will be two dodecahedra such that the intersection of their vertex sets are the vertices of this cube, and we can find the axes of each of the other four cubes that fit in each of those two dodecahedra as the column vectors of:

$$R^k, S^k, \qquad k=1,2,3,4 $$

where \(R\) and \(S\) are two order-5 rotations. We can continue this process iteratively, alternating between powers of \(R\) and \(S\):

$$ R^k S^\ell ,\; S^k R^\ell ,\; R^k S^\ell R^m ,\; S^k R^\ell S^m , \dots$$

where the powers range from 1 to 4, to generate all the cubes in all the dodecahedra in the tree of twins.

We claim that the cube axes that result from applying \(N \ge 1\) rotations (along with their opposite vectors), contain exactly one copy of each unit vector over the golden field that can be written as:

$$ \frac{1}{2^{N+1}} (a + b \sqrt{5}, c + d \sqrt{5}, e + f \sqrt{5}) $$

where \(a, b, c, d, e, f\) are integers and at least one of them is odd. In that sense, the vector is written ‘in lowest terms’: there are no factors that can be cancelled in the denominator and in all the numerators.

For \(N=0\), the results don’t conform to this pattern. There are no unit vectors over the golden field that can be written in lowest terms with a denominator of \(2^1\). Rather, the original axes, which is what we have for \(N=0\), involve a denominator of \(2^0\).

Proof. We have some freedom in choosing $R$ and $S$, but this makes no difference to the resulting sets of axes. We will pick:

$$\displaystyle{R = \frac{1}{4} \left(
\begin{array}{ccc}
2 & 1-\sqrt{5} & -1-\sqrt{5} \\
1-\sqrt{5} & 1+\sqrt{5} & -2 \\
1+\sqrt{5} & 2 & -1+\sqrt{5} \end{array} \right)}$$

$$\displaystyle{S = \frac{1}{4} \left(
\begin{array}{ccc}
\sqrt{5}-1 & -2 & -1-\sqrt{5} \\
2 & 1+\sqrt{5} & 1-\sqrt{5} \\
1+\sqrt{5} & 1-\sqrt{5} & 2 \end{array}\right)}$$

All the powers of these matrices can again be written with a denominator of 4 and numerators taken from \(\{\pm 2, \pm 1 \pm \sqrt{5}\}\). That the 48 vectors obtained by taking the columns of these eight matrices, and their opposites, include all the unit vectors over the golden field with a denominator of 4 can be verified by a direct computation, since there are only a finite number of possible candidates to check.

We will simplify things a bit by working with integer matrices in 6 dimensions. For each of the four powers of \(R\) and \(S\), we will multiply the matrix by 4 and then write it as a linear map between 6-dimensional spaces with separate components for the rational and irrational parts of each component of the original vector. For example, for the first power of \(R\) we get:

$$ R_6 = \left(
\begin{array}{cccccc}
2 & 0 & 1 & -5 & -1 & -5 \\
0 & 2 & -1 & 1 & -1 & -1 \\
1 & -5 & 1 & 5 & -2 & 0 \\
-1 & 1 & 1 & 1 & 0 & -2 \\
1 & 5 & 2 & 0 & -1 & 5 \\
1 & 1 & 0 & 2 & 1 & -1 \end{array}\right)$$

and for the first power of \(S\) we get:

$$ S_6 = \left(
\begin{array}{cccccc}
-1 & 5 & -2 & 0 & -1 & -5 \\
1 & -1 & 0 & -2 & -1 & -1 \\
2 & 0 & 1 & 5 & 1 & -5 \\
0 & 2 & 1 & 1 & -1 & 1 \\
1 & 5 & 1 & -5 & 2 & 0 \\
1 & 1 & -1 & 1 & 0 & 2 \end{array}\right)$$

Suppose we have some unit vector \(v\) of the form:

$$ v = \frac{1}{2^{N+1}} (a + b \sqrt{5}, c + d \sqrt{5}, e + f \sqrt{5}) $$

where \(a, b, c, d, e, f\) are integers, with at least one of them odd, and \(N \ge 1\). We will work with the integer vector:

$$w = (a, b, c, d, e, f) $$

Because \(v\) is a unit vector, the components of \(w\) will satisfy the conditions:

$$ a^2 + c^2 + e^2 + 5(b^2 + d^2 + f^2) = 4^{N+1}$$

and

$$ a b + c d + e f = 0$$

If we multiply any vector of this form by each of the eight 6 × 6 matrices corresponding to the four powers of \(R\) and \(S\), then it turns out that precisely one of those eight matrices will yield a result equal to the zero vector modulo 8, i.e. a 6-tuple of integers all divisible by 8.

We can prove this by explicitly checking a finite number of cases in \((\mathbb{Z} /8)^6\) and using the homomorphism that maps vectors of integers to the vector of their residue classes modulo 8. Given any vector \(w\) in \(\mathbb{Z}^6\) that meets our conditions, its image \((A,B,C,D,E,F)\) under that homomorphism will meet the conditions:

$$ A^2 + C^2 + E^2 + 5(B^2 + D^2 + F^2) = 0 \mod 8 $$

and

$$A B + C D + E F = 0 \mod 8$$

Also, at least one of these integers will be odd. A direct computation with the 3072 vectors in \((\mathbb{Z} / 8)^6 \) meeting these conditions shows that in every case, precisely one of the eight integer matrices corresponding to the powers of \(R\) and \(S\) yields the zero vector, modulo 8.

Because \(R\) and \(S\) are rotations of order 5, the set of their first 4 powers can also be seen as the set of inverses of their first 4 powers. Because the corresponding integer matrices are multiplied by a factor of 4, a result that is a multiple of 8 corresponds to a factor of 2 in the original matrices. So what we have established is that, given any unit vector over the golden field with a denominator of \(2^{N+1}\) for some \(N \ge 1\), the inverse of precisely one of the powers of \(R\) and \(S\) will take us to another unit vector with a denominator of \(2^N\). As we repeat this process, we will move back through the tree to ever smaller denominators, eventually terminating with the original cube.

This means that we can reach every unit vector \(v\) of this form as one of the cube axes or their opposites, and also that we can only reach it via a single path.   █

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!