Catacaustic of a Cardioid – Greg Egan

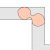
This image, drawn by Greg Egan, shows a cardioid and its catacaustic.

The cardioid is a heart-shaped curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. The catacaustic of a curve in the plane is the envelope of rays emitted from some source and reflected off that curve.

If we shine rays from the cusp of the cardioid, the resulting catacaustic is a curve called the nephroid. This is the curve traced by a point on the perimeter of a circle that is rolling around a fixed circle whose radius is twice as big!

Does this pattern continue? What is the catacaustic of a nephroid? And in general, given an algebraic curve of degree $d$, what can we say about the degree of its catacaustic? If you get stuck on these puzzles, see:

• Greg Egan, Catacaustics, resultants and kissing conics.

For more on cardioids, nephroids and other curves formed by rolling one circle on another, see:

• John Baez, Rolling circles and balls.

It’s worth mentioning that we can get the nephroid as a catacaustic in another way, too: by shining light on a circle from a point at infinity, and letting the rays bounce off the inside of the circle.

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!