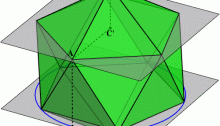
Origami Dodecahedra
There is a nice photograph of some interlocking origami dodecahedra created by Dirk Eisner on the website Mathematical Origami. But it’s hard to be sure how many dodecahedra the whole model contains, since some are hidden from view. This raises a puzzle: assuming the configuration is as symmetrical as possible, how many dodecahedra are there? Here you see Greg Egan’s answer to this puzzle—and to a much more challenging puzzle.