Zero Set of Discriminant of Restricted Quintic – Greg Egan
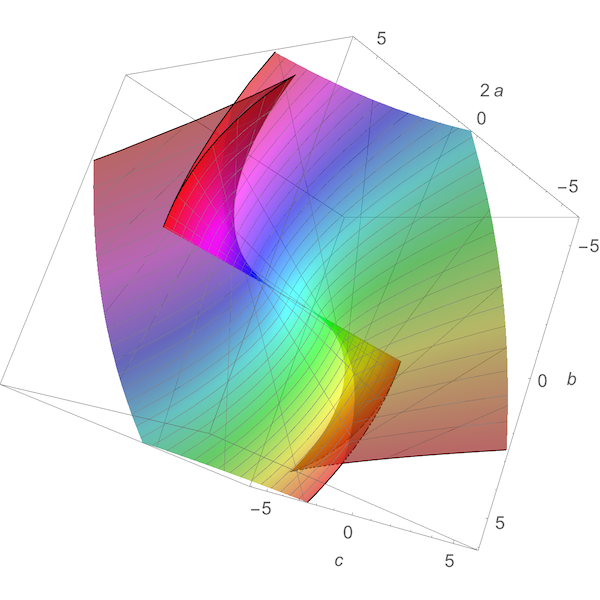
This image by Greg Egan shows the set of points \((a,b,c)\) for which the quintic \(x^5 + ax^4 + bx^2 + c \) has repeated roots. The plane \(c = 0\) has been removed.
The fascinating thing about this surface is that it appears to be diffeomorphic to two other surfaces, defined in completely different ways, which we discussed here:
• Involutes of a cubical parabola.
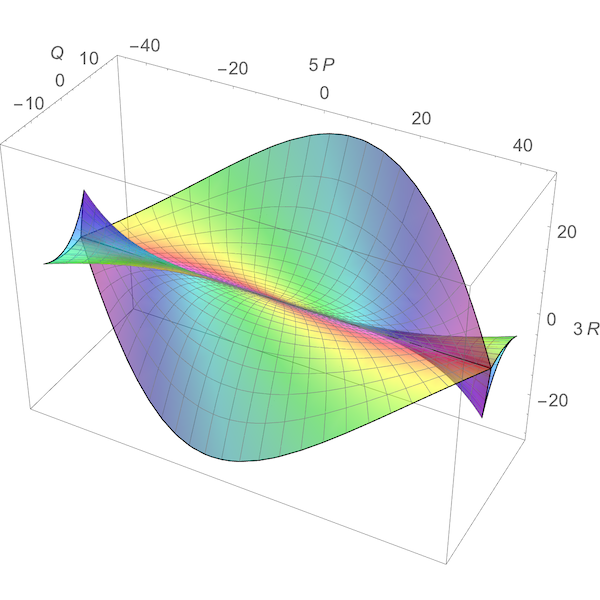
• Discriminant of the icosahedral group.
The icosahedral group is also called \(\mathrm{H}_3\). In his book The Theory of Singularities and its Applications, V. I. Arnol’d writes:
The discriminant of the group \(\mathrm{H}_3\) is shown in Fig. 18. Its singularities were studied by O. V. Lyashko (1982) with the help of a computer. This surface has two smooth cusped edges, one of order 3/2 and the other of order 5/2. Both are cubically tangent at the origin. Lyashko has also proved that this surface is diffeomorphic to the set of polynomials \(x^5 + ax^4 + bx^2 + c\) having a multiple root.
Figure 18 of Arnold’s book is a hand-drawn version of the surface below:
\(\mathrm{H}_3\) Discriminant – Greg Egan
Arnol’d’s claim that the discriminant of \(\mathrm{H}_3\) is diffeomorphic to the set of polynomials \(x^5 + ax^4 + bx^2 + c\) having a repeated root is not literally true, since all such polynomials with \(c = 0\) have a repeated root, and we need to remove this plane to obtain a surface that looks like the discriminant of \(\mathrm{H}_3\). After this correction his claim seems right, but it still deserves proof.
Puzzle. Can you prove the corrected version of Arnol’d’s claim?
References
Arnol’d’s claim appear on page 29 here:
• Vladimir I. Arnol’d, The Theory of Singularities and its Applications, Cambridge U. Press, Cambridge, 1991.
The following papers are also relevant:
• Vladimir I. Arnol’d, Singularities of systems of rays, Uspekhi Mat. Nauk 38:2 (1983), 77-147. English translation in Russian Math. Surveys 38:2 (1983), 77–176.
• O. Y. Lyashko, Classification of critical points of functions on a manifold with singular boundary, Funktsional. Anal. i Prilozhen. 17:3 (1983), 28–36. English translation in Functional Analysis and its Applications 17:3 (1983), 187–193
• O. P. Shcherbak, Singularities of a family of evolvents in the neighbourhood of a point of inflection of a curve, and the group \( \mathrm{H}_3\) generated by reflections, Funktsional. Anal. i Prilozhen. 17:4 (1983), 70–72. English translation in Functional Analysis and its Applications 17:4 (1983), 301–303.
• O. P. Shcherbak, Wavefronts and reflection groups, Uspekhi Mat. Nauk 43:3 (1988), 125–160. English translation in Russian Mathematical Surveys 43:3 (1988), 1497–194.
All these sources discuss the discoveries of Arnol’d and his colleagues relating singularities and Coxeter–Dynkin diagrams, starting with the more familiar \(\mathrm{ADE}\) cases, then moving on to the non-simply-laced cases, and finally the non-crystallographic cases related to \(\mathrm{H}_2\) (the symmetry group of the pentagon), \(\mathrm{H}_3\) (the symmetry group of the icosahedron) and \(\mathrm{H}_4\) (the symmetry group of the 600-cell).
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!
Can Klein’s method for solving the quintic be adapted to eliminate \(x^2\) & \(x^2\) terms instead of \(x^4\) & \(x^3\)?
I don’t know. I have thought about how the special class of quintics discussed here ($x^5+ax^4+bx^2+c = 0$) is related to the special classes that show up when people try to solve the quintic, but I haven’t any good ideas yet! Klein’s ideas are especially tempting, because they involve the icosahedron. But still, I don’t see what’s going on.
An explicit diffeomorphism between the three-dimensional space of invariants of the icosahedral symmetry group $(P,Q,R)$ and the coefficients $(a,b,c)$ of the restricted quintics that maps the discriminant into the discriminant is given by:
$(a,b,c) = (P, \alpha Q + \beta P^3, \gamma R + \delta Q P^2 + \epsilon P^5)$
where the constants $\alpha, \beta, \gamma, \delta, \epsilon$ depend on the precise choice of normalisation for the invariants $P, Q, R$. If we recall that those invariants (defined here) are homogeneous polynomials of degree 2, 6 and 10 in the coordinates $x, y, z$, this diffeomorphism is the simplest kind of map that is consistent with the fact that $a, b, c$ are homogenous polynomials of degree 1, 3 and 5 in the roots of the quintic. It’s not hard to see that this map has a constant, non-zero Jacobian determinant, which proves that it is a diffeomorphism, and in fact it has a polynomial inverse of the same general form.
The five constants $\alpha, \beta, \gamma, \delta, \epsilon$ can be determined by identifying three curves that appear in both discriminant surfaces, the lines of cusps of type 5/2 and 3/2 and the line of double points, which all take the general parametric form $(a, A_i a^3, B_i b^5)$ or $(P, C_i P^3, D_i P^5)$, with four of the constants here equal to zero, in those cases where the curve in question is a straight line along a coordinate axis.
Excellent! So the Puzzle is solved!
Although the particular diffeomorphism depends on the choice of normalisation for the invariants $P,Q,R$ of the icosahedral symmetry group, it’s possible to make the following identification that remains true regardless of that choice.
If $e_1$ and $e_2$ are two orthogonal unit vectors that pass through edge centres of the icosahedron, then the point on the mirror plane:
$m = \sqrt{\frac{1}{2}\left(\left(1+\frac{1}{\sqrt{5}}\right) a + \sqrt{5} \alpha \right)} e_1 + \sqrt{\frac{1}{2}\left(\left(1-\frac{1}{\sqrt{5}}\right) a – \sqrt{5} \alpha \right)} e_2$
when mapped to the invariant space $(P,Q,R)$ and then to the space of quintics $(a,b,c)$ corresponds to the restricted quintic with a coefficient of $a$ for the degree-4 term and a repeated root of $\alpha$.