Which shape is worst of all for packing the plane? That is, which has the lowest maximal packing density?

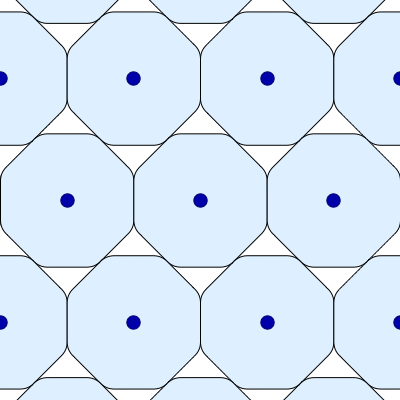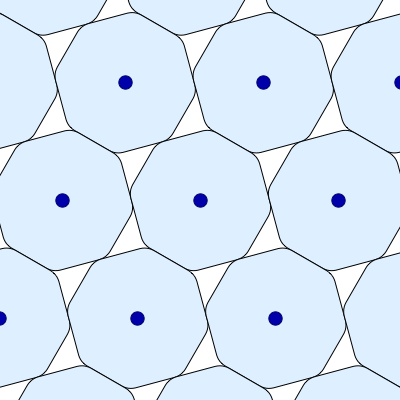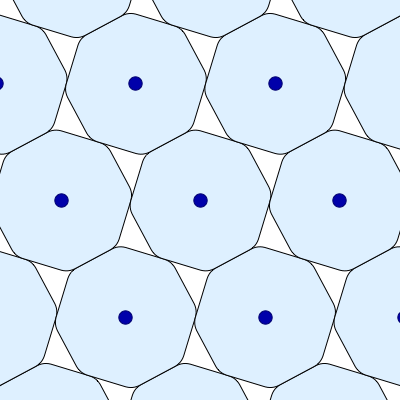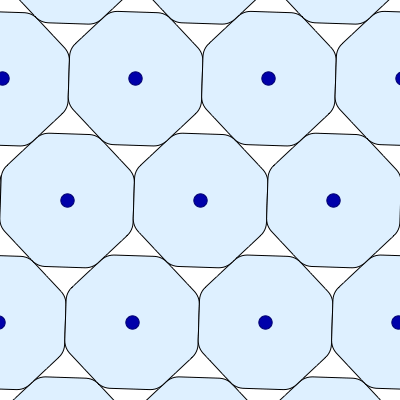
If we allow shapes that are not convex, we can get arbitrarily low maximal packing densities. Among convex shapes, the regular heptagon is conjectured to be the worst. But suppose we demand that our shape be convex and also centrally symmetric: that is, a subset $S \subseteq \mathbb{R}^2$ such that $x \in S$ implies $-x \in S$. Then a certain ‘smoothed octagon’ is conjectured to be the worst. Amazingly, this shape has a 1-parameter family of maximally dense packings, shown in this image created by Greg Egan.

As mentioned in our previous post:

• Packing regular octagons.

the advantage of convex centrally symmetric bounded open nonempty sets in the plane is that Fejér Thoth and Rogers proved that for any such shape, there is a maximally dense packing that is a lattice packing: all copies of the shape are translates of a single one by vectors in some lattice.

One example is the disk, which has maximum packing density of

$$ \frac{\pi}{\sqrt{12}} = 0.9068996 \dots $$

The regular octagon has a slightly smaller maximal packing density:

$$ \frac{4 + 4 \sqrt{2}}{5 + 4 \sqrt{2}} = 0.9061636 \dots $$

However, if we smooth the corners of the regular octagon in a specific way, we get a maximum packing density of only

$$ \frac{ 8-4\sqrt{2}-\ln{2} }{2\sqrt{2}-1} = 0.902414 \dots $$

In 1934, Reinhardt conjectured this shape was the worst among all convex centrally symmetric sets:

• K. Reinhardt, Über die dichteste gitterförmige Lagerung kongruenter bereiche in der ebene und eine besondere art konvexer Kurven, Abh. Math. Sem. Hamburg 10 (1934), 216–230.

How do we choose how to smooth the octagon? We do it so there is a 1-parameter family of maximally dense lattice packings, where the octagons ‘roll’ around a central one! Greg Egan has explained how this works:

Here’s a derivation of the shape of the smoothed octagon’s corners, starting from the assumption that the packing density remains constant as the figure rotates.

Suppose we begin with regular octagons of width 2. That is, the distance from the centre to the midpoint of each edge is 1. Then if we rotate the octagons shown in the animation in the previous comment by an angle $\theta$, keeping the bottom-left octagon’s centre fixed at $(0,0)$, the bottom-right octagon’s centre will move to $(2 \sec(\theta),0)$ in order for the edges to continue to make contact along a line segment.

The top octagon’s centre will move to:

$$\left(\frac{\sec(\theta+\pi/4)}{\sqrt{2}} – \left(2\sqrt{2}-1\right)\sin(\theta), \left(2\sqrt{2}-1\right)\cos(\theta)\right)$$

in order that it also has an edge that lies flush against one of the bottom-left octagon’s edges, and that the area of the triangle formed by the three octagons’ centres remains constant.

A vector that goes halfway from the top octagon’s centre to the bottom-right octagon’s centre is given by:

$$P=\left(\sec(\theta)-\frac{\sec(\theta+\pi/4)}{2\sqrt{2}}+\left(\sqrt{2}-\frac{1}{2}\right)\sin(\theta),-\left(\sqrt{2}-\frac{1}{2}\right)\cos(\theta)\right)$$

This takes us to the point that traces out the smoothed corner of the octagon.

If we re-express $P$ in a basis that rotates along with the top octagon, with our new x-axis pointing to the vertex that overlaps with the bottom-right octagon, and we change our parameter from $\theta$ to $t=\tan(\theta)$, we obtain:

$$x(t) = \cos \left(\frac{\pi }{8}\right) t+\frac{\csc \left(\frac{\pi }{8}\right)}{4 (t-1)}+\sin \left(\frac{\pi
}{8}\right)+\frac{1}{2} \csc \left(\frac{\pi }{8}\right)$$
$$y(t) = -\sin \left(\frac{\pi }{8}\right) t +\frac{\left(\sqrt{2}-1\right) \csc \left(\frac{\pi
}{8}\right)}{4 (t-1)}+\sin \left(\frac{\pi }{8}\right)$$

It’s not hard to eliminate $t$ from these equations, which gives us the hyperbola:

$$y^2 = \left(3-2 \sqrt{2}\right) \left(x-\csc \left(\frac{\pi }{8}\right)\right)^2-\sqrt{2}+1$$

As we follow the parameterised curve from $t=0$ to $t=1-\frac{1}{\sqrt{2}}$, $x(t)$ returns to its starting value, and $y(t)$ to the opposite of its starting value, completing the corner.

We can’t continue to use the same functions of $\theta$ as the coordinates for the centres of the three octagons for larger values of $\theta$ than $\tan ^{-1}\left(1-\frac{1}{\sqrt{2}}\right)$, because beyond that point the bottom octagons begin to make contact along smoothed corners rather than the original flat edges. But the shape we’ve found for those smoothed corners and the symmetry of the figures guarantees that we can *maintain the constant area* of the triangle formed by the three octagon centres, as $\theta$ continues through a full rotation.

Thomas Hales, who proved the Kepler conjecture, has an NSF grant based on a proposal where he says he will prove Reinhardt’s conjecture:

In 1934, Reinhardt considered the problem of determining the shape of the centrally symmetric convex disk in the plane whose densest packing has the lowest density. In informal terms, if a contract requires a miser to make payment with a tray of identical gold coins filling the tray as densely as possible, and if the contract stipulates the coins to be convex and centrally symmetric, then what shape of coin should the miser choose in order to part with as little gold as possible? Reinhardt conjectured that the shape of the coin should be a smoothed octagon. The smoothed octagon is constructed by taking a regular octagon and clipping the corners with hyperbolic arcs. The density of the smoothed octagon is approximately 90 per cent. Work by previous researchers on this conjecture has tended to focus on special cases. Research of the PI gives a general analysis of the problem. It introduces a variational problem on the special linear group in two variables that captures the structure of the Reinhardt conjecture. An interesting feature of this problem is that the conjectured solution is not analytic, but only satisfies a Lipschitz condition. A second noteworthy feature of this problem is the presence of a nonlinear optimization problem in a finite number of variables, relating smoothed polygons to the conjecturally optimal smoothed octagon. The PI has previously completed many calculations related to the proof of the Reinhardt conjecture and proposes to complete the proof of the Reinhardt conjecture.

This research will solve a conjecture made in 1934 by Reinhardt about the convex shape in the plane whose optimal packing density is as small as possible. The significance of this proposal is found in its broader context. Here, three important fields of mathematical inquiry are brought to bear on a single problem: discrete geometry, nonsmooth variational analysis, and global nonlinear optimization. Problems concerning packings and density lie at the heart of discrete geometry and are closely connected with problems of the same nature that routinely arise in materials science. Variational problems and more generally control theory are have become indispensable tools in many disciplines, ranging from mathematical finance to robotic control. However, research that gives an exact nonsmooth solution is relatively rare, and this feature gives this project special interest among variational problem. This research is also expected to further develop methods that use computers to obtain exact global solutions to nonlinear optimization problems. Applications of nonlinear optimization are abundant throughout science and arise naturally whenever a best choice is sought among a system with finitely many parameters. Methods that use computers to find exact solutions thus have the potential of finding widespread use. Thus, by studying this particular packing problem, mathematical tools may be further developed with promising prospects of broad application throughout the sciences.

Here is another image of the smoothed octagon’s densest packings, also created by Greg Egan and put on Wikicommons with a Creative Commons Attribution-Share Alike 3.0 Unported license. In this version, the orientation of each smoothed octagon remains fixed:

Another advantage of convex centrally symmetric bounded open nonempty sets in $\mathbb{R}^n$ is that these are precisely the sets that arise as an open ball for some norm. And in fact the moduli space of norms on $\mathbb{R}^n$ is a compact space, called the Banach–Mazur compactum. Since the maximal packing density defines a continuous function on the Banach–Mazur compactum, there must be a convex centrally symmetric bounded open nonempty set that minimizes this function.

For more details, try these:

• Thomas Hale, On the Reinhardt conjecture.

• Yoav Kallus, Least efficient packing shapes.

• John Baez, A packing pessimization problem, The n-Category Café.

• Smoothed octagon, Wikipedia.

The last page has a formula for the boundary of the smoothed octagon, illustrated with some figures.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!