Densest Packing of Regular Octagons – Graeme McRae

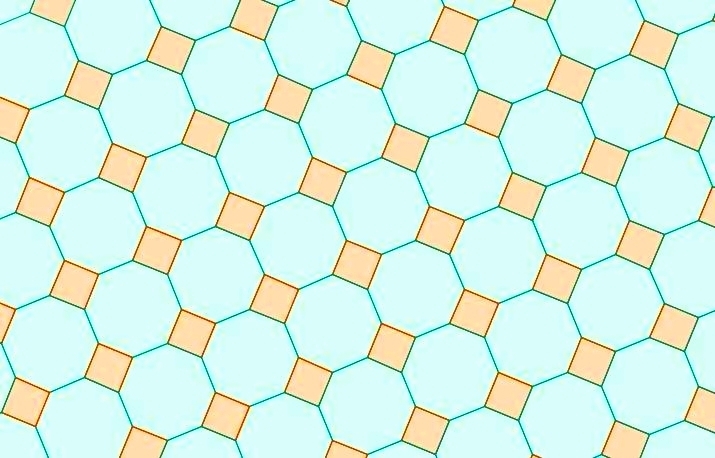
This is the densest packing of regular octagons in the plane, drawn by Graeme McRae. It is interesting because it is a counterexample to the 2-dimensional analogue of a conjecture made in 3 dimensions by Stanislaw Ulam.

Ulam’s packing conjecture states that of all convex bodies in 3d Euclidean space, the ball has the smallest maximum packing density. Since congruent balls can be packed with a density of

$$ \frac{\pi}{\sqrt{18}} = 0.74048048… $$

and Kepler’s conjecture, now a theorem, says this is a best possible, Ulam’s conjecture says that for any other convex body in $\mathbb{R}^3$, we can pack congruent copies of this body with a density more than $\pi/\sqrt{18}$.

The analogous conjecture in 2 dimensions would say that every convex region in the Euclidean plane can be packed with a density at least

$$ \frac{\pi}{\sqrt{12}} = 0.9068996… $$

However, the densest packing of regular octagons, shown above, has density only

$$ \frac{4 + 4 \sqrt{2}}{5 + 4 \sqrt{2}} = 0.9061636… $$

It density is only about $.0007$ less, but this suffices to refute the conjecture!

There is another more famous packing of regular octagons, the truncated octagonal tiling:

Truncated Square Tiling – Turmamataplicada

but this is far from the most dense. One obtains the densest packing by shifting each row of octagons enough to push them into the gaps left by the neighboring row.

That the packing drawn by Graeme McRae is the densest possible packing of regular octagons is asserted here:

• Steven Atkinson, Yang Jiao and Salvatore Torquato, Maximally dense packings of two-dimensional convex and concave noncircular particles, Phys. Rev. E 86 (2012), 031302.

I have not actually seen the proof, but it may use a result of László Fejes Tóth and C. A. Rogers, that the densest packing of congruent copies of any convex region in the plane possessing central symmetry is achieved by a lattice structure, with all copies being translates of a given one:

• C. A. Rogers, The closest packing of convex two-dimensional domains, Acta Math. 86 (1951), 309–321. Erratum, 104 (1960), 305–306.

• László Fejes Tóth, Some packing and covering theorems, Acta Sci. Math. 12A (1950), 62–67.

This reduces the problem of finding the densest packing of regular octagons to the problem of maximizing a function on a finite-dimensional space, namely the space of lattices.

The picture of the truncated octagonal tiling was made by ‘Turmamataplicada’ and put onto Wikimedia Commons with a Creative Commons Attribution-Share Alike 3.0 Unported license.

The convex centrally symmetric region with the lowest maximal packing density is conjectured to be a smoothed version of the regular octagon. We’ll discuss that in the next post:

• Packing smoothed octagons.

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!