2-adic Integers – Christopher Culter
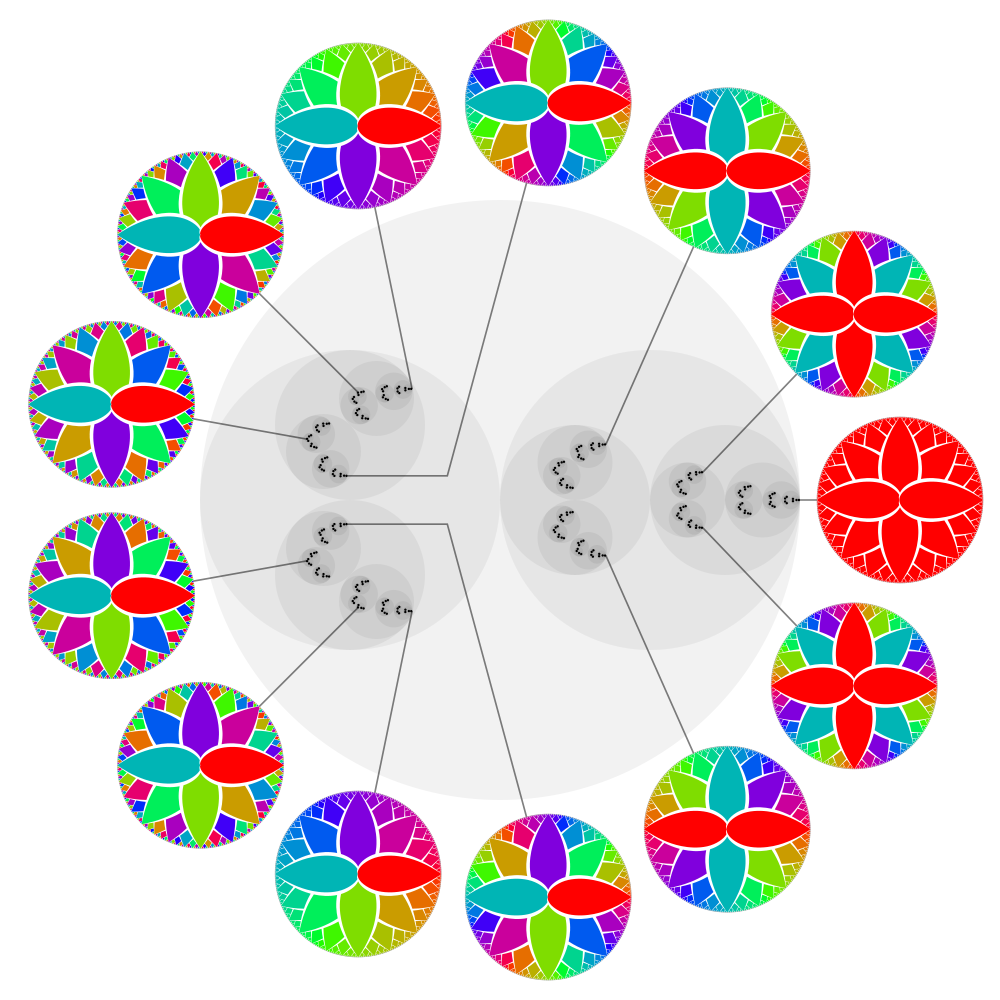
This image created by Christopher Culter shows the compact abelian group of 2-adic integers (black points), with selected elements labeled by the corresponding character on the Pontryagin dual group (colored discs).
Counterclockwise from the right, the labeled elements are
$$ 0, 4, 2, −3, 1, −\frac{1}{7}, -\frac{1}{3}, \frac{1}{3}, \frac{1}{7}, −1, 3, −2, -4 $$
The Pontryagin dual of the group of 2-adic integers is the Prüfer 2-group $\mathbb{Z}(2^\infty)$. See our earlier article
for an explanation of that. Each colored disc here is tied to a 2-adic integer, $x\in\mathbb{Z}_2$, and it represents a character
$$ \chi_x : \mathbb{Z}(2^\infty) \to \mathbb{R}/\mathbb{Z}$$
defined by
$$ \chi_x(q) = x q.$$
Points in the circle $\mathbb{R}/\mathbb{Z}$ are drawn using a color wheel where $0$ is red, $\frac{1}{3}$ is green, and $\frac{2}{3}$ is blue.
For details on the embedding of the 2-adic integers in the plane, see:
• D. V. Chistyakov, Fractal geometry for images of continuous embeddings of $p$-adic numbers and $p$-adic solenoids into Euclidean spaces, Theoretical and Mathematical Physics 109 (1996), 1495–1507
The particular mapping used is $\Upsilon_s^{(\infty)}$, defined in Definition 3 and depicted in Figure 1.12 of this paper.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!
