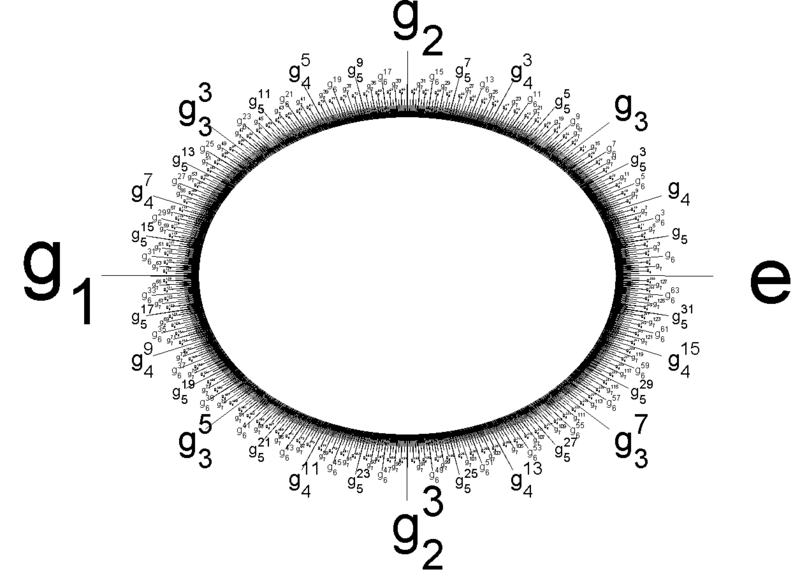
This is the Prüfer 2-group, the subgroup of the unit complex numbers consisting of all 2nth roots of unity. It is also called Z(2∞). It is generated by elements
g1=eiπ=−1,g2=eiπ/2=i,g3=eiπ/4,g4=eiπ/8,…
with relations
g2n+1=gn,g21=1
In the picture, elements are labelled by their names in terms of these generators.
In general, for any prime p the Prüfer p-group is the subgroup of the unit circle consisting of all pnth roots of unity:
Z(p∞)={e2πim/pn:m,n=1,2,3,…}
We can also think of the Prüfer p-group as a subgroup of Q/Z, namely the group consisting of all equivalence classes of fractions where the denominator is a power of p.
More abstractly, we can think of the Prüfer p-group as the colimit of the groups
Z/pZ→Z/p2Z→Z/p3Z→⋯
As a Z-module, the Prüfer p-group is Artinian. This means that that any infinite descending sequence of subgroups of the Prüfer p-group ‘bottoms out’ after finitely many steps. On the other hand, it is not Noetherian: there are infinite ascending sequences of subgroups that keep getting bigger forever. So, it is a good example to distinguish the concepts of ‘Artinian’ and ‘Noetherian’.
The Prüfer p-group can be given a topology induced from the usual topology on the circle, but it can also be given the discrete topology. With its discrete topology, it is the Pontryagin dual of the compact abelian group of p-adic integers. We will explore this more in the next article.
This image is from Wikicommons, where it was placed into the public domain by its creator, known only as Anon213487. I have no idea why the unit circle is drawn as an ellipse here, but it’s sort of cute.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!




Should that be ; i..e. the third
; i..e. the third 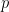 is cubed? Abstract question… if we think of the subgroup relation as an orthogonal cut, is it possible in some sense to cut diagonally across these subgroups and create an ordered set which also bottoms out?
is cubed? Abstract question… if we think of the subgroup relation as an orthogonal cut, is it possible in some sense to cut diagonally across these subgroups and create an ordered set which also bottoms out?