The Zamolodchikov tetrahedron equation, illustrated above by J. Scott Carter and Masahico Saito, is a fundamental law governing surfaces embedded in 4-dimensional space. It also arises purely algebraically in the theory of braided monoidal 2-categories.
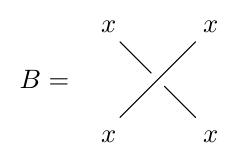
Given an object x in a monoidal category, we say a morphism
B:x⊗x→x⊗x
obeys the Yang–Baxter equation if
(B⊗1)(1⊗B)(B⊗1)=(1⊗B)(B⊗1)(1⊗B)
We can understand this using the technique of string diagrams if we draw B as a ‘braiding’, the process of switching two copies of the object x:
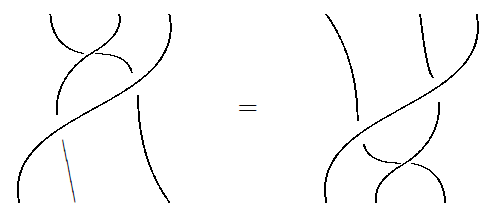
The Yang–Baxter equation then says this:
In other words, we can slide a crossing of two strands under a third strand. In topology this is called the third Reidemeister move, one of three basic ways of changing a picture of a knot without changing the topology of the knot.
Given an object x in a monoidal 2-category and a morphism
B:x⊗x→x⊗x,
we can demand that the Yang–Baxter equation hold up to a 2-morphism. This means that there is a 2-morphism
Y:(B⊗1)(1⊗B)(B⊗1)⇒(1⊗B)(B⊗1)(1⊗B)
called the Yang–Baxterator. We think of this as the process of sliding a crossing of strands under a third strand:
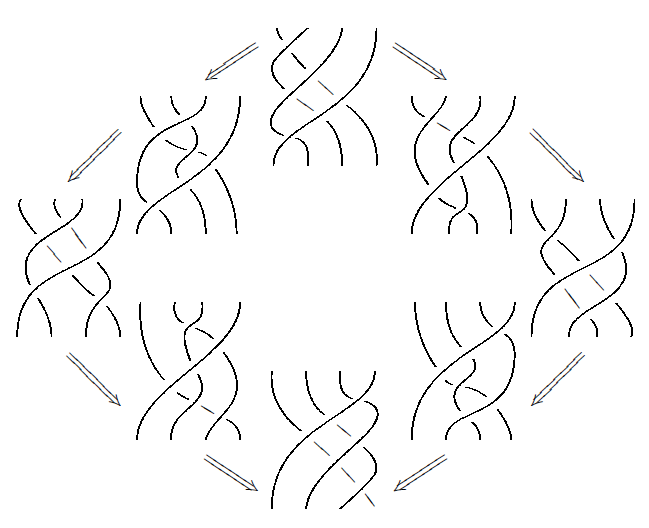
Using topology, we can see that it is natural for the Yang–Baxterator to satisfy an equation of its own, a higher-dimensional analogue of the Yang–Baxter equation. This is called the Zamolodchikov tetrahedron equation:
[Y∘(1⊗1⊗B)(1⊗B⊗1)(B⊗1⊗1)][(1⊗B⊗1)(B⊗1⊗1)∘Y∘(B⊗1⊗1)][(1⊗B⊗1)(1⊗1⊗B)∘Y∘(1⊗1⊗B)][Y∘(B⊗1⊗1)(1⊗B⊗1)(1⊗1⊗B)]=[(B⊗1⊗1)(1⊗B⊗1)(1⊗1⊗B)∘Y][(B⊗1⊗1)∘Y∘(B⊗1⊗1)(1⊗B⊗1)][(1⊗1⊗B)∘Y∘(1⊗1⊗B)(1⊗B⊗1)][(1⊗1⊗B)(1⊗B⊗1)(B⊗1⊗1)∘Y].
To see the significance of this complex but beautifully symmetrical equation, one should think of Y as the surface in 4-dimensional space traced out by the process of performing the third Reidemeister move. Then the Zamolodchikov tetrahedron equation says the surface traced out by first performing the third Reidemeister move on a threefold crossing and then sliding the result under a fourth strand:
can be deformed to the surface traced out by first sliding the threefold crossing under the fourth strand and then performing the third Reidemeister move:
So, the Zamolodchikov tetrahedron equation says this:
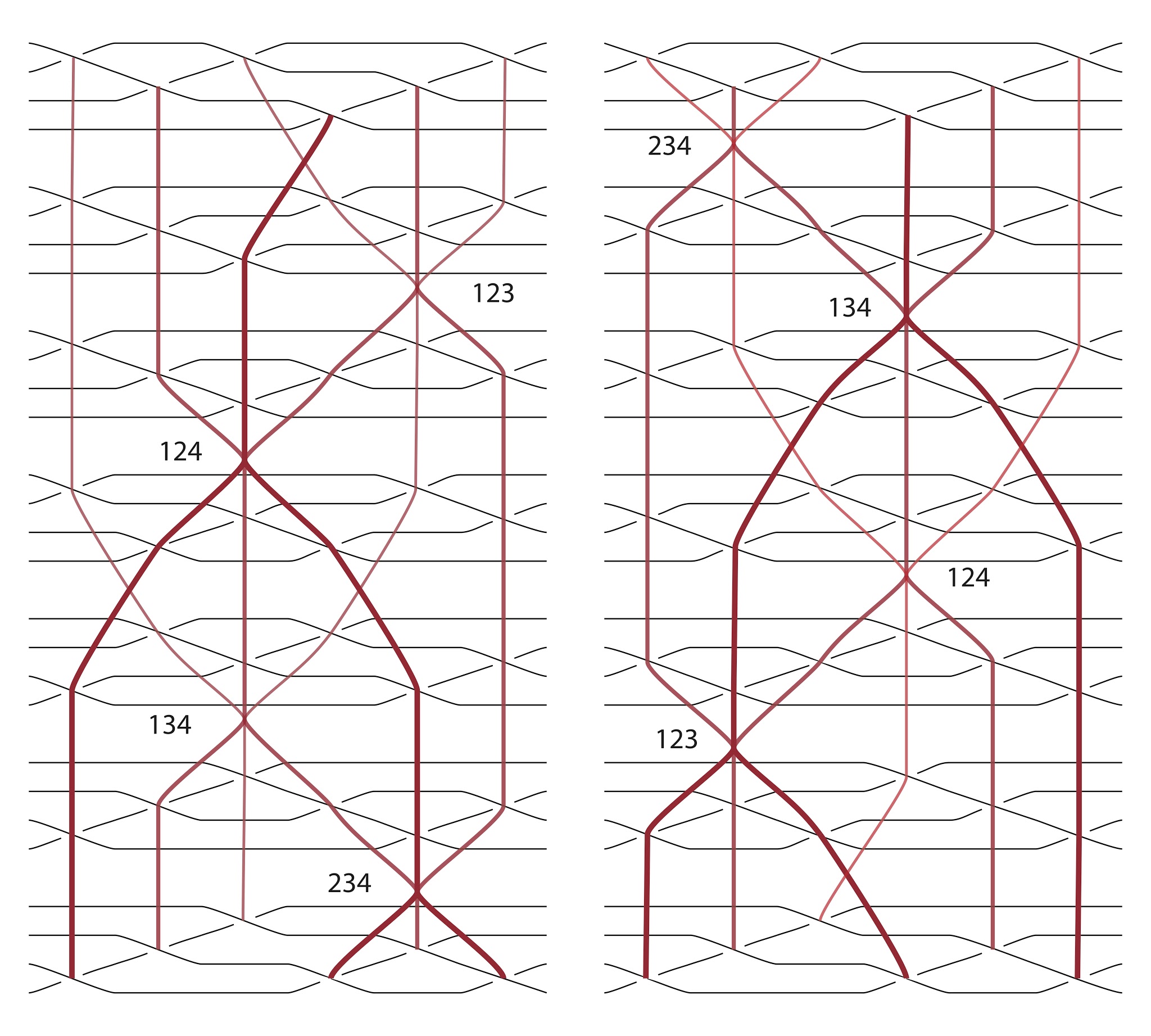
Here is another picture of it created by Carter and Saito:
The numbers indicate which three strands are involved in each appearance of the Yang–Baxterator.
To learn more about the role of the Zamolodchikov tetrahedron equation in topology, see these papers:
• J. Scott Carter, Seiichi Kamada and Masahico Saito, Surfaces in 4-Space, Springer, Berlin, 2004.
• J. Scott Carter and Masahico Saito, Knotted Surfaces and Their Diagrams, AMS, Providence, Rhode Island, 1998.
Just as the Yang–Baxter equation is a consequence of the definition of braided monoidal category, the Zamolodchikov tetrahedron equation automatically follows from the definition of ‘braided monoidal 2-category’. For details and connections to other algebraic structures, see:
• John Baez and Martin Neuchl, Higher-dimensional algebra I: braided monoidal 2-categories, Adv. Math. 121 (1996), 196–244.
• Sjoerd Crans, Generalized centers of braided and sylleptic monoidal 2-categories, Adv. Math. 136 (1998), 183–223.
• John Baez and Laurel Langford, Higher-dimensional algebra IV: 2-tangles, Adv. Math. 180 (2003), 705–764.
• John Baez and Alissa Crans, Higher-dimensional algebra VI: Lie 2-algebras, Theory and Applications of Categories, 12 (2004), 492–528.
The uncaptioned pictures above come from the paper by Baez and Crans; most of them were created by Aaron Lauda.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!

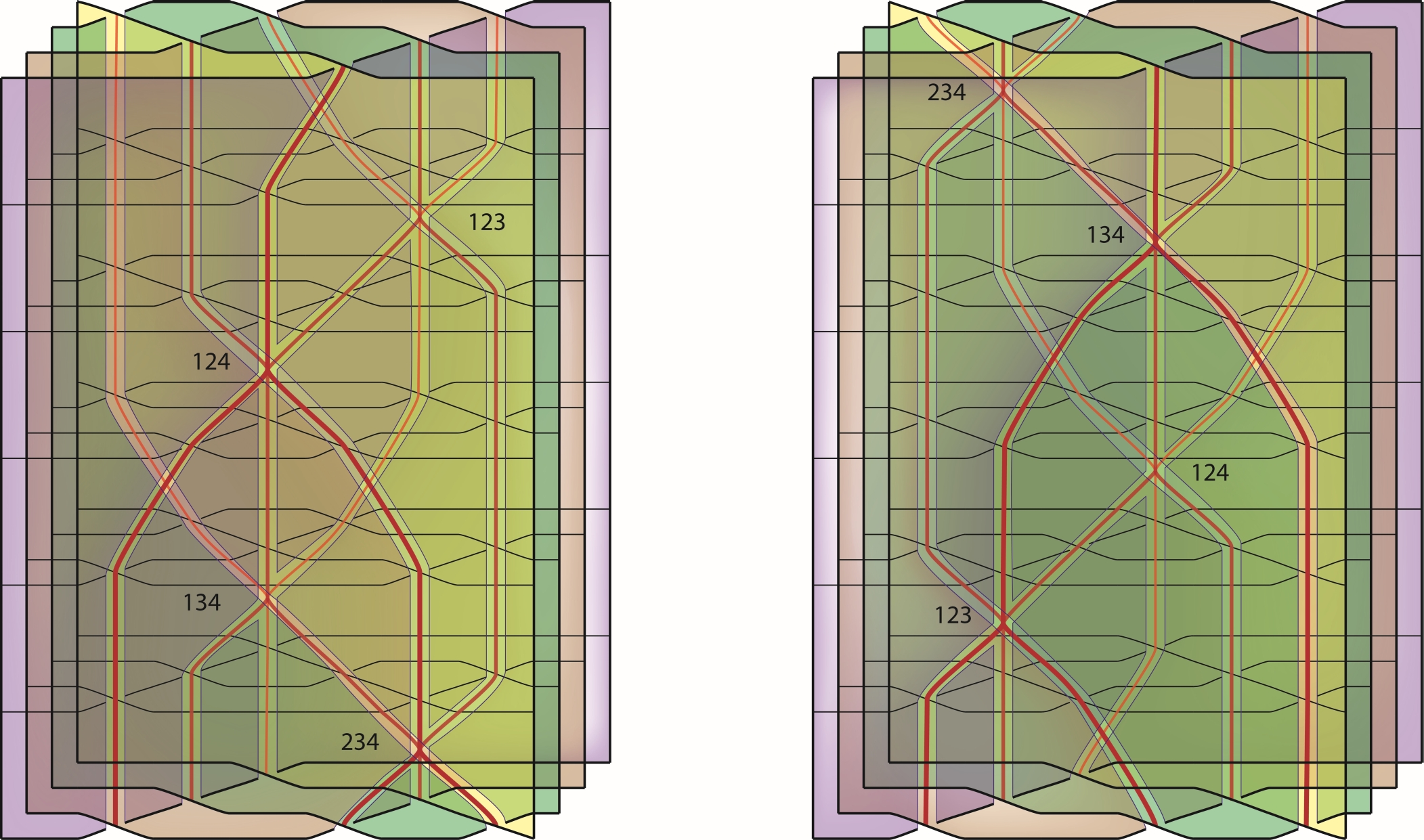
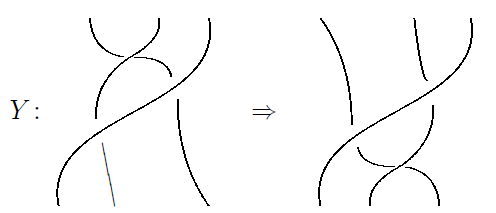

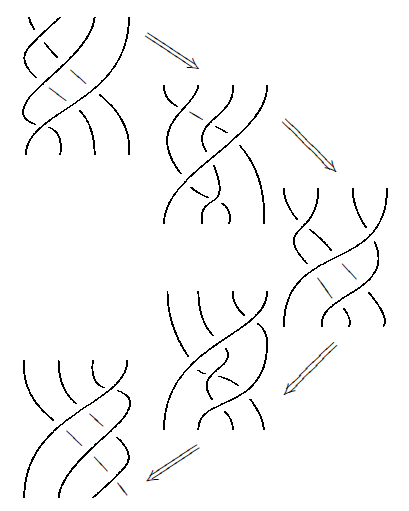



The thickness of the strands in the left-hand image at the top seems to be the opposite way around to the right-hand image: thicker red lines seem to be in front in the latter, which makes more sense, and fainter ones behind other sheets. The left-hand image is the other way around.
Yes, you are correct about that. I used a very useful symmetry to make the drawing: Namely, if I rotate the 2dimensional image 180 degrees, the resulting movie on the other side appears. I did so with the red lines. On the second, clear, illustration, I fixed the resulting line thicknesses, but I forgot to do so on the shaded version.
Scott fixed it!
Excellent! Thanks, Scott (and John for the hosting)
It would be really nice if the strands were colored.
Dear Tim,
Thanks for the suggestion. The illustration was originally drawn for another purpose in which I needed the given color, line thickness, and degree of transparency denote double points at various levels.
Scott
I think I wasn’t clear. The main image is great. I mean the black and white images below. Adding color coding to the strands there will make it easier to follow. .
The black and white diagrams aren’t Scott’s fault. They’re from an old paper I wrote with Alissa Crans. We didn’t have color in those days: the whole world was in black and white.
Yes mommy doesn’t look too happy in front of the dishes. But then Daddy is at least busy with keeping Calvin away from more messing and stressing.
I think I read this post when you first posted it, but came back to it just now after your recent mention on G+… and I just realized, staring at the second-to-last image here, that this equation has 180-degree rotational symmetry; if you turn the commutative diagram upside-down and reverse all the arrows, you get the same diagram!
I’m sure I’m not the first person to notice this, and it doesn’t seem terribly exciting, but it is kind of cute.
Yes, it’s cute! Surfaces in 4d space need to obey both equations — the original and the one rotated by 180 degrees — so perhaps it’s a relief that they’re the same.
Thomas, It is true that I drew one by rotating the other. I was happy to do so because the drawing is a bit tedious. But front to back switches, and David’s comment above about thickness was the fault of a mere rotation.
Ah! And if I’d read your comment above I would have seen you mention exactly this symmetry, whoops 🙂 Goes to show what happens when I’m overly focused on the pretty pictures….