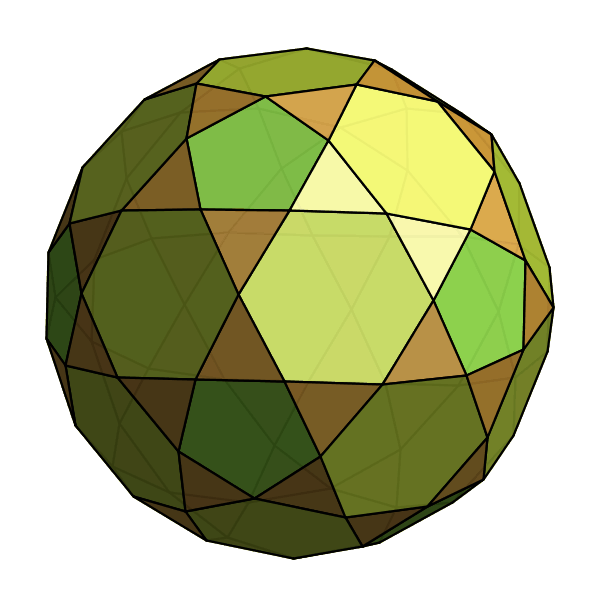
The rectified truncated icosahedron is a surprising new polyhedron discovered by Craig S. Kaplan. It has 60 triangles, 12 pentagons and 20 hexagons as faces. For a rotating view, see:

• Greg Roelofs, Rectified truncated icosahedron.

This polyhedron can be obtained by first truncating the icosahedron (cutting off its corners) and then rectifying the result: that is, cutting off all the newly formed corners so that the newly formed faces actually meet.

An Archimedean solid is a convex polyhedron composed of two or more types of regular polygons meeting in identical vertices. By convention, prisms and antiprisms are not considered to be Archimedean solids. Until the 20th century, only 13 Archimedean solids were known, or 15 if the two mirror image forms of the snub cube and snub dodecahedron are counted separately.

In 1905, the elongated square gyrobicupola was discovered by Duncan Sommerville. Whether this counts as an Archimedean solid or not depends on the precise definition of the concept: each vertex looks locally like every other vertex, but there do not exist symmetries of the whole solid carrying each vertex to each other vertex.

Most mathematicians have adopted the more restrictive definition, in which an Archimedean solid is a convex polyhedron, with two or more types of regular polygons of faces, whose symmetry group (including both rotations and reflections) acts transitively on the vertices. The elongated square gyrobicupola is considered a Johnson solid: a convex polyhedron where the faces are all regular polygons but the symmetry group does not act transitively on the vertices.

Johnson solids are named after Norman Johnson, who in 1966 published a list of 92 such solids. He conjectured that this list was complete, but did not prove it. In 1969, Viktor Zalgaller published a proof that Johnson’s list was complete.

It thus came as a huge shock to the mathematical community when Craig Kaplan, a computer scientist at the University of Waterloo, discovered an additional Johnson solid in 2001: the rectified truncated icosahedron! At the time, he was compiling a collection of ‘near misses’: polyhedra that come very close to being Johnson solids.

In an interview with the New York Times, he said:

When I found this one, I was impressed at how close it came to being a Johnson solid. But then I did some calculations, and I was utterly flabbergasted to discover that the faces are exactly regular! I don’t know how people overlooked it.

It turned out there was a subtle error in Zalgaller’s lengthy proof.

Here is a rotating view of the rectified truncated icosahedron created by Greg Roelofs:

April Fools! The text in purple above is false, while the rest is correct. In fact, the rectified truncated icosahedron is not a Johnson solid: it’s a near miss. If you look carefully you can see that the triangles are not equilateral.

The pentagons and hexagons, on the other hand, are perfectly regular. This explains why the triangles cannot also be equilateral: if they were, the polyhedron would need to be flat — lie in a plane — at vertices where two triangles and two hexagons meet, since

You can see more near misses here:

• Craig S. Kaplan, Near misses.

• Craig S. Kaplan and George W. Hart, Symmetrohedra: polyhedra from symmetric placement of regular polygons, in Bridges 2001: Mathematical Connections in Art, Music and Science, 2001.

• Jim McNeil, Near miss polyhedra.

After discovering the rectified truncated icosahedron, Kaplan realized that this solid may have been discovered as early as 1568. Take a look and decide for yourself:

• Daniele Barbaro, La Pratica Della Perspettiva, 1568, page 97.

Daniele Barbaro was an Italian cardinal best known for his translations of Vitruvius. But he studied philosophy, mathematics, and optics at the University of Padua, and his book La Pratica Della Perspettiva is a manual of perspective which also describe how to use a lens with a camera obscura. The drawing above appears to be designed to create a fold-up model of the rectified truncated icosahedron!

Johnson’s list of polytopes can be found here:

• Norman W. Johnson, Convex polyhedra with regular faces, Canadian Journal of Mathematics 18 (1966), 169–200.

Zalgaller’s proof first appeared here:

• Viktor A. Zalgaller, Vypuklye mnogogranniki s pravilʹnymi grani︠a︡mi, Zap. Nauchn. Semin. Leningr. Otd. Mat. Inst. Steklova 2 (1966), 1–221.

and was later reprinted here:

• Viktor A. Zalgaller, Convex Polyhedra With Regular Faces, Seminars in Mathematics, V. A. Steklov Mathematics Institute, vol. 1, Consultants Bureau, New York, 1969.

The images of the clockwise snub cube was created by Cyp and placed on Wikicommons under a GNU Free Documentation License. The counterclockwise one was created by applying a left-right reflection. The image of the elongated square gyrobicupola was created by Andrew Kepert and placed on Wikicommons under a Creative Commons Attribution-Share Alike 3.0 Unported license.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!