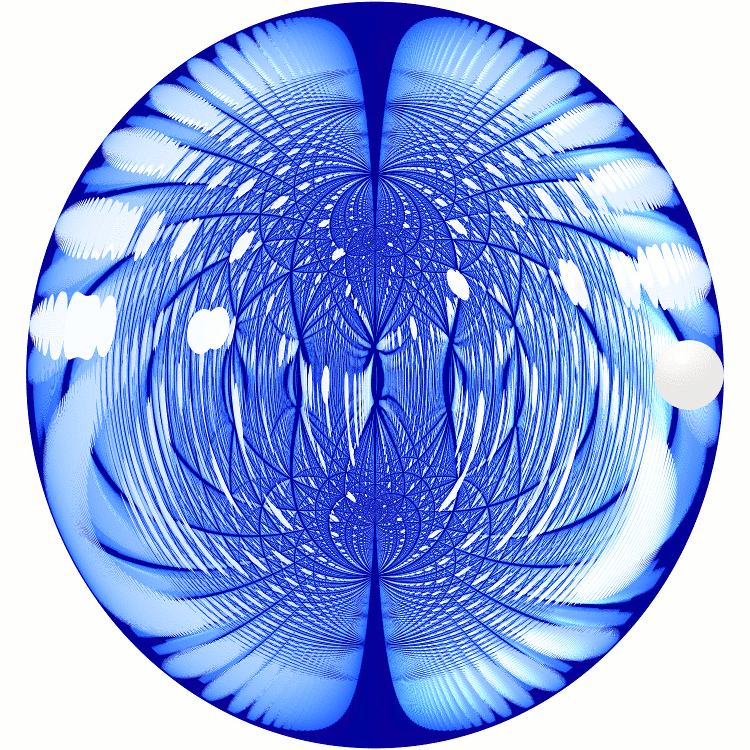
Sphere in Mirrored Spheroid – Refurio Anachro

A spheroid is an ellipsoid with an axis of rotational symmetry. This image created by Refurio Anachro shows a sphere inside a mirrored spheroid, together with its reflections. For some beautiful multicolored closeups of this picture, see below.

He explains:

This is about billiards in a rotationally symmetric ellipsoid. Ludwig Boltzmann famously invented statistical mechanics by thinking of atoms as billiard balls. Emil Artin examined billiards in the hyperbolic plane. Later, George Birkhoff considered billiards on a table whose border is infinitely differentiable.

Since then, many other billiards have been studied as examples of ‘chaotic’ dynamical systems. Physicists are using quantum billards to study the way microwaves bounce in them, and, following Artin, they appear in some theories about the early universe. And there is plenty of literature on ellipsoidal billiards as well…

The picture shows (half of) the inside of a mirrored prolate spheroid, 10% taller than it is wide. The pattern is made of reflections of the little white marble you can see on the right hand side. To the slightly bluish mirror it appears pure white, but I have shaded the unreflected marble afterwards to make it easier to identify.

More precisely, the marble is a sphere, with radius a tenth that of the equatorial circle of the spheroid, and touching it there from the inside. I’ve placed it 90° away from one of the two ‘straight’ positions to make the image less symmetric and more interesting.

The idea behind the marble was that we could pick a point and highlight all rays coming close to it. But the presence of the marble changes things: since it extends into the spheroid, it will catch high flying rays that might not have gotten reflected in the vicinity of our chosen point. Coloring a patch of the spheroid’s surface, or punching a hole in it, would not have produced some rather beautiful artifacts you see here.

That large, wavy, most bright reflection to the left, and all the similar ones, would resolve to a number of separate elongated images of our spot. And the smaller blots further inside, the biggest one looking like two intersecting elliptic discs, would look more like a single one. And the marble-thick, brighter appearing region all around the rim.

Aside from that, the marble works like a flashlight. Think of the pattern as a fixed, static thing, produced by all possible rays bouncing within the ellipsoid. Moving the flashlight will illuminate different parts of it. Some points will be especially hard to illuminate. Two of them are the foci of the prolate spheroid: they’re the the dark points that appear to attract reflections that can never reach them, just above and below the center.

To further avoid vertical symmetry, the camera was rotated below the equatorial plane by about 22.62°. That’s 3 steps back and 2 steps down from the center it is looking at.

The camera does an orthographic projection, where all the projection lines are orthogonal to the projection plane. It is somewhat surprising that the image isn’t much different from ones obtained by a perspective projection with the camera sitting on the surface. Note that while a perspective projection can always be smoothly deformed to the orthographic one, just by sending the viewpoint to infinity, our sampling points, which previously corresponded to different ray angles, will now correspond to different starting positions!

It is even more fascinating when you look at it like this. Trying to understand the paths, we can play an easier game with a flat ellipse, studying its set of all reflecting paths. It’s known that those decompose topologically into two classes, and a set of borderline cases that separate them. But what I want to get at is this: Not only does the turning direction always stay the same for a path, there’s a conserved quantity for the paths. This ensures that a path that starts out skimming the surface of the ellipse will never become one that jumps far away from it.

For a three-dimensional prolate spheroid we get two conserved quantities, but just one class of solutions. Here’s a paper John sent me. It has cool 3d images of paths, and a nice overview of a partial classification:

• Pablo S. Casas and Rafael Ramirez-Ros, Classification of symmetric periodic trajectories in ellipsoidal billiards.

But the pattern we see also depends on the elevation angle of the camera! Standing close to the poles we’d see many concentric rings. Looking from the equatorial plane we would get larger, and more vertically stretched structures along the equator line. There clearly is a similarity to the two modes of the ellipse at work here.

To that end, I made an animation sliding the camera from pole to equator here:

• The physical ellipse — how can Hamiltonians help to understand billiards in spheroids?

Above, I mentioned a conserved quantity for a billiard bouncing within an ellipse—a quantity that, like energy, does not change with time. What is it? To specify a path, we have to give a point where it hits the ellipse together with the reflection angle at some point. The former clearly changes on each reflection, but the latter may as well. Now we have to find a function of these two variables that remains constant as we go from any reflection point to the next reflection point on the same path. This will be our conserved quantity. A value of this quantity picks out a 1-dimensional submanifold out of our 2-dimensional space of paths, and the successive reflections of our billiard define a sequence of points that stay in the same submanifold.

Today, physicists attack such problems with Langrangian or Hamiltonian mechanics. It’s what the authors did in the following paper, also suggested to me by John:

• Peter H. Richter, Andreas Wittek, Mikhail P. Kharlamov and Alexej P. Kharlamov, Action integrals for ellipsoidal billiards.

The method involves some heavy machinery, but it is also a beautiful supplement to basic calculus that I’d like to invite everyone to play with. It took me some time to understand that, as a bookkeeping device meant to track, for example, the exchange between two forms of energy happening while a ball rolls downhill along a continuous path, this machinery also applies when the path hops from place to place, as the contact points of our light rays do. We already know how to reflect a ray as it hits the mirror’s surface to find the next point it will hit. What we can learn using Hamiltonian and Lagrangian mechanics is the global structure of ray’s possible paths, the structure of the energy surfaces.

If you want to try this for a billiard in an ellipse you first need to find action-angle coordinates, or in other words, a coordinate system that is ‘separable’. In a typical classical mechanics problem this means, for example, that the total energy can be written as a sum where each summand depends only on one of the coordinates, so that explicitly solving the equations of motion becomes a reasonable thing to wish for.

In our case it is even simpler, because there is no potential energy term. Nevertheless the resulting problem will involve elliptic integrals, and we know their solutions cannot be written down using elementary functions. We need elliptic functions.

As the name ‘elliptic function’ suggests, it is no surprise they occur here. If you try to compute the arc length of an ellipse, you’ll run into one of these integrals right away. Of the heroes of this story it was Carl Gustav Jacob Jacobi who first found a nice way to handle them, to name them, and put rhythm and rhyme to them.

Here are some more links. First, a simple starting point to get in touch with billiards:

• W. Patrick Hooper and Richard Evan Schwartz, Billiards in nearly isosceles triangles.

I have written a number of posts about Hamiltonians, ellipses, billiards, and other related stuff. Let me highlight an animation showing the ‘feathers’ that appear in the above image, and
some higher resolution pictures:

• A set of high resolution views, and an animation of iteration depth for raytraced spheroidal billiards.

By the way, the feathers appear to be cut off, and while I’m not certain they’re not an artifact produced by the limitations of floating point arithmetic, zooming in shows they’re made of many fingers.

If you want to play with the scenery yourself, here’s a direct link to a file for the Persistence of Vision Raytracer:

• POV-ray traced billiards in spheroids.

The following images were made by John Valentine. Now the ball is lit from three directions with soft red, green, and blue lights, so we can see things more clearly. The view simulates an ultra-wide-angle camera. The black regions arise because the ray-tracing program only allows 256 reflections; they would get smaller if more reflections were allowed.

Sphere in Mirrored Spheroid: Closeup 1 – John Valentine

Here is another view:

Sphere in Mirrored Spheroid: Closeup 2 – John Valentine

These are just portions of a much bigger picture! You can get other views here, along with a good discussion:

• John Valentine, Endless reflections, 16 April 2015.

You can get John Valentine’s really big version here. This is 16384 × 16384 pixels and about 16 megabytes. If you know a nice way to display such a big image online, which makes it easy to zoom in on pieces, please try it and let me know!

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!