Suppose we inscribe a regular pentagon, a regular decagon, and a regular hexagon in circles of the same radius. If we denote the respective edge lengths of these polygons by P, D and H, then these lengths satisfy the identity
P2=D2+H2
This means that the edges of a pentagon, decagon and hexagon of identical radii can fit together to form a right triangle!
Euclid stated this beautiful but mysterious identity as Proposition 10 of Book XIII of the Elements. This is the last book of the Elements, the one which deals with properties of the Platonic solids. He used Proposition 10 as part of his construction of the regular icosahedron in Proposition 13.
This has led some historians to suggest that the pentagon-decagon-hexagon identity was first discovered in the course of research on the icosahedron. The idea is this. If you hold an icosahedron so that one vertex is on top and one is on bottom, you’ll see that its vertices are arranged in 4 horizontal layers. From top to bottom, these are:
- 1 vertex on top
- 5 vertices forming a pentagon: the "upper pentagon"
- 5 vertices forming a pentagon: the "lower pentagon"
- 1 vertex on bottom
Pick a vertex from the upper pentagon: call this A. Pick a vertex as close as possible from the lower pentagon: call this B. A is not directly above B. Drop a vertical line down from A until it hits the horizontal plane on which B lies. Call the resulting point C:
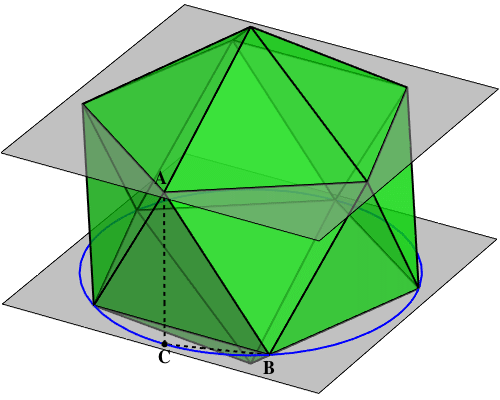
It is easy to check that ABC is a right triangle. If we apply the Pythagorean theorem to this triangle we get the equation
P2=D2+H2
But to see this, we need to check that:
- the length AB equals the edge of a pentagon inscribed in a circle;
- the length AC equals the edge of a hexagon inscribed in a circle;
- the length BC equals the edge of a decagon inscribed in a circle.
Different circles, but of the same radius! What’s this radius? The five vertices of the lower pentagon lie on the circle shown in blue. This circle has the right radius.
Using this idea, it’s easy to see that the length AB equals the edge of a pentagon inscribed in a circle. It’s also easy to see that BC equals the edge of a decagon inscribed in a circle of the same radius. The hard part is showing that AC equals the edge of a hexagon inscribed in a circle of the same radius… or in other words, the radius of that circle! (The hexagon appears to be a red herring.)
To prove this, it suffices to show the following marvelous fact: the distance between the "upper pentagon" and the "lower pentagon" equals the radius of the circle containing the vertices of the upper pentagon!
Can you prove this?
In Ian Mueller’s book Philosophy of Mathematics and Deductive Structure in Euclid’s Elements, he suggested various ideas the Greeks could have had about this. Today’s image shows one. Let’s look at it again:
The trick is to construct a new right triangle AB′C′. Here B′ is the top vertex, and C′ is where a line going straight down from B′ hits the plane containing the upper pentagon.
Remember, we’re trying to show the distance between the upper pentagon and lower pentagon
equals the radius of the circle containing the vertices of the upper pentagon.
But that’s equivalent to showing that AC′ is congruent to AC.
To do this, it suffices to show that the right triangles ABC and AB′C′ are congruent! Can you do it?
In the references to Mueller’s book, he says the historians Dijksterhuis (in 1929) and Neuenschwander (in 1975) claimed this is “intuitively evident”. He also notes that Eva Sachs, in her book Die Fünf Platonischen Körper, suggested an accurately drawn figure could let someone guess that the distance between the two pentagons equals the radius of either one. But that’s not a proof.
You can see a proof due to Greg Egan here:
• Pentagon-hexagon-decagon identity: Proof using the icosahedron, nLab.
Egan put some other proofs of the pentagon-hexagon-decagon identity here:
• Pentagon-hexagon-decagon identity, nLab.
Also see:
• John Baez, This Week’s Finds in Mathematical Physics, Week 283, and discussion on the n-Category Café.
• Eva Sachs, Die Fünf Platonischen Körper, zur Geschichte der Mathematik und der Elementenlehre Platons und der Pythagoreer, Berlin, Weidmann, 1917, pp. 102–104. See page 102–103 here and page 104 here.
• Ian Mueller, Philosophy of Mathematics and Deductive Structure in Euclid’s Elements, MIT Press, Cambridge Massachusetts, 1981, pp. 257–258 and references therein.
Of course, we can prove also prove the pentagon-hexagon-decagon identity using algebra. Start with a unit circle. If we inscribe a regular hexagon in it, then clearly
H=1
So we just need to compute P and D. If we think of the unit circle as living in the complex plane, then the solutions of
z5=1
are the corners of a regular pentagon. So let’s solve this equation. We’ve got
0=z5–1=(z–1)(z4+z3+z2+z+1)
so ignoring the dull solution z=1, we must solve
z4+z3+z2+z+1=0
This says that the center of mass of the pentagon’s corners lies right in the middle of the pentagon.
Now, quartic equations can always be solved using radicals, but it’s a lot of work. Luckily, we can solve this one by repeatedly using the quadratic equation! And that’s why the Greeks could construct the regular pentagon using a ruler and compass.
The trick is to rewrite our equation like this:
z2+z+1+z−1+z−2=0
and then like this:
(z+z−1)2+(z+z−1)−1=0
If we write
z+z−1=x
our equation becomes
x2+x–1=0
Solving this, we get two solutions. One of them is the golden ratio
x=ϕ=√5−12≈0.6180339…
Next we need to solve
z+z−1=ϕ
This is another quadratic equation:
z2–ϕz+1=0
with two conjugate solutions, one being
z=ϕ+√ϕ2–42
This is a fifth root of unity in the first quadrant of the complex plane, so we know
z=exp(2πi/5)=cos(2π/5)+isin(2π/5)
So, we’re getting
cos(2π/5)=ϕ/2
A fact we should have learned in high school, but probably never did! Now we’re ready to compute P, the length of the side of a pentagon inscribed in the unit circle:
P2=|1–z|2=(1–cos(2π/5))2+sin2(2π/5)=2–2cos(2π/5)=2–ϕ
Next let’s compute D, the length of the side of a decagon inscribed in the unit circle! We can mimic the last stage of the above calculation, but with an angle half as big:
D2=2–2cos(π/5)
To go further, we can use the half-angle formula:
cos(π/5)=√1+cos(2π/5)2=√12+ϕ4
This gives
D2=2–√2+ϕ
But we can simplify this a bit more. As any lover of the golden ratio should know,
2+ϕ≈2.6180339…
is the square of
1+ϕ≈1.6180339…
So we really have
D2=1–ϕ
And now we’re done! We see that the pentagon-hexagon-decagon identity
P2=D2+H2
simply says:
2–ϕ=1+(1–ϕ)
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!




