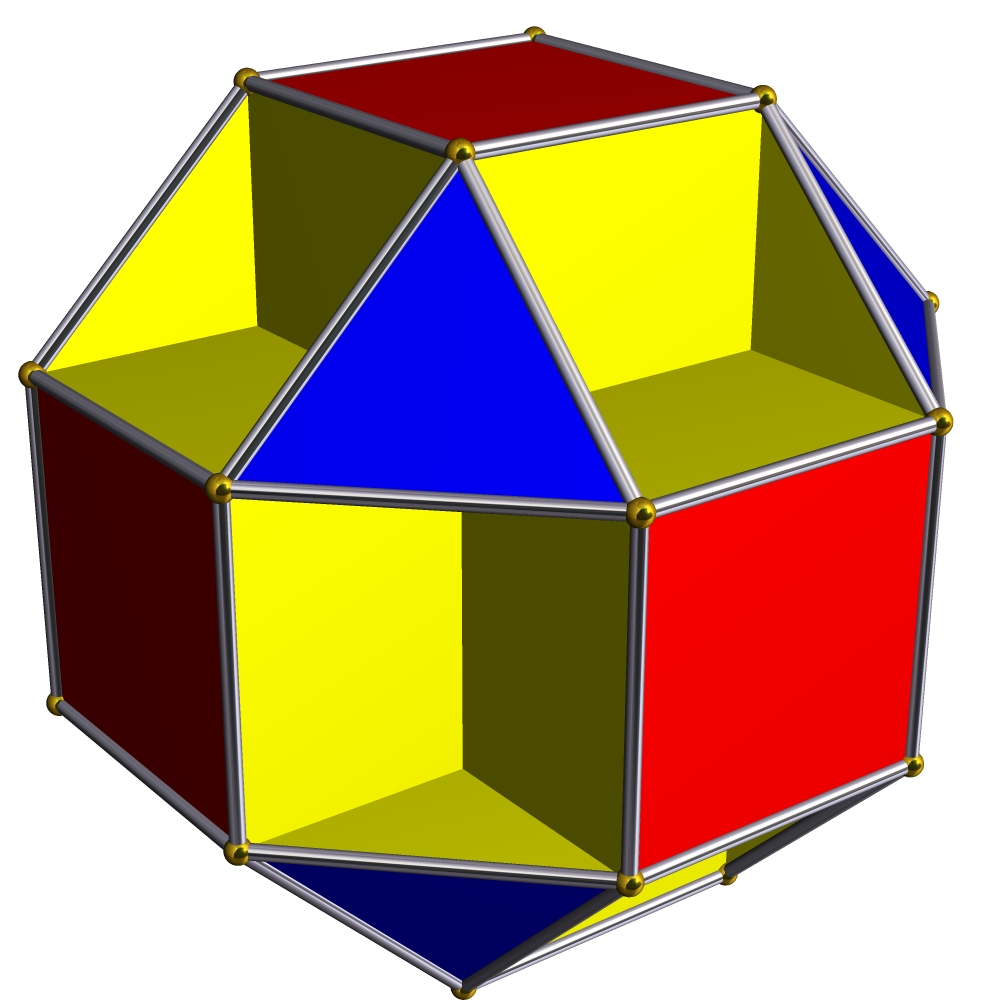
This is the small cubicuboctahedron, as drawn by Robert Webb’s Great Stella software. It looks simple enough, but it conceals some interesting mathematics.
For starters, the yellow pieces are actually regular octagons which are mostly hidden from view. The three shades of yellow are parts of three octagons, but there are also three more, each parallel to a plane containing a red square. Thus, this polytope has 3 kinds of faces:
• 6 red squares,
• 8 blue equilateral triangles, and
• 6 yellow octagons.
Don’t be fooled by how the octagons cross each other. That creates ‘false edges’ that are not considered edges of this polytope.
As you trace out a small loop traversing all the faces that meet at a vertex, crossing edges and ignoring false edges, you traverse first a square, then an octagon, a triangle, then another octagon… and finally you return to where you started. Your path is a small figure 8.
So, this polytope has regular polygons as faces, and every corner looks like every other: more precisely, its symmetry group acts transitively on the vertices. It is thus considered a uniform polyhedron. But it’s not convex, and it has faces that cross other faces, forming false edges! It is thus called a uniform star polyhedron.
You can study the small cubicuboctahedron intrinsically—ignoring the false edges, and treating it as a manifold built by gluing together polyhedra. Then it’s actually a 3-holed torus. To see this, note that it is orientable, with:
• 20 faces, since there are 8 triangles, 6 squares and 6 octagons,
• 48 edges, since no two octagons have a common edge and no triangle or square has a common edge with another triangle or square, making the number of edges equal to 8 times the number of octagons,
• 24 vertices, since every vertex is the corner of a square and no two squares share a vertex, making the number of vertices equal to 4 times the number of squares.
By Euler’s formula, the genus g of the small cubicuboctahedron satisfies
2–2g=V–E+F=24–48+20=−4
so g=3, making it a 3-holed torus. We may view it abstractly as a piecewise-linear manifold, but it is not embedded in R3, because it crosses itself along the ‘false edges’.
This is just the beginning of an interesting story. For more on the topology, combinatorics and group theory of uniform star polyhedra, see:
• Zvi Har’El, Uniform solution for uniform polyhedra, Geometriae Dedicata 47 (1993), 57–110.
• Uniform star polyhedron, Wikipedia
Next time we’ll delve a bit deeper into this story:
• Branched cover from (4432) Schwarz triangle.
The image above was placed on Wikimedia Commons by Tom Ruen, and the copyright holder of this file allows anyone to use it for any purpose, provided that acknowledgement is given to Robert Webb’s Great Stella software as the creator of this image along with a link to the Stella website.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!




Glad to see this figure discussed.
I made a paper model which shows that your yellow face planes are “golden” rectangles, and how this small cubicuboctahedron can be inscribed inside a regular octahedron, and your blue face planes will be co-planar with the octahedron. Further, these triangles will also be co-planar with the icosahedron that can be inscribed in the octahedron.
I have photos if you want to see.
SW
I’d be happy to see them!