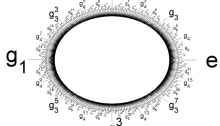
Schmidt Arrangement

This picture drawn by Katherine Stange shows what happens when we apply fractional linear transformations $ z \mapsto \frac{a z + b}{c z + d} $ to the real line sitting in the complex plane, where $a,b,c,d$ are Eisenstein integers that is, complex numbers of the form $ m + n \exp(2 \pi i/3) $ with $m,n$ being integers.

2-adic Integers

This image created by Christopher Culter shows the compact abelian group of 2-adic integers (black points), with selected elements labeled by the corresponding character on the Pontryagin dual group (colored discs).

Prüfer 2-Group

This is the Prüfer $2$-group, the subgroup of the unit complex numbers consisting of all $2^n$th roots of unity. It is also called $\mathbb{Z}(2^\infty)$.

Algebraic Numbers

This is a picture of the algebraic numbers in the complex plane, made by David Moore based on earlier work by Stephen J. Brooks. Algebraic numbers are roots of polynomials with integer coefficients. In this picture the color indicates the degree of the polynomial.