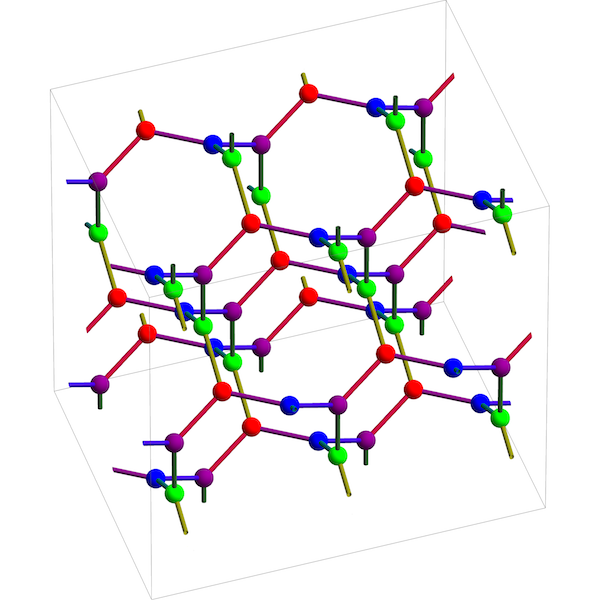
This picture by Greg Egan shows the Laves graph, a structure discovered by the crystallographer Fritz Laves in 1932. It is also called the ‘\(\mathrm{K}_4\) crystal’, since is an embedding of the maximal abelian cover of the complete graph on 4 vertices in 3-dimensional Euclidean space. It is also called the ‘triamond’, since it is a theoretically possible — but never yet seen — crystal structure for carbon.

In the Laves graph, each vertex is connected to three others with edges at 120° angles. These edges lie in a plane, so we get a plane for each atom. However, for any two neighboring vertices, these planes are different. In fact, these planes come in four equally spaced families, parallel to the four faces of a regular tetrahedron.

The Laves graph is highly symmetrical. There is a symmetry carrying any vertex and any of its edges to any other vertex and any of its edges. However, the Laves graph has an inherent handedness, or chirality: it comes in two different mirror-image forms.

The smallest cycles in the Laves graph have 10 edges. Each vertex lies in 15 of these 10-cycles.

Some chemists have argued that the triamond should be ‘metastable’ at room temperature and pressure: that is, it should last for a while but eventually turn to graphite. Diamonds are also considered metastable. However, diamonds are formed naturally under high pressure — while triamonds, it seems, are not.

Nonetheless, the mathematics behind the Laves graph does find its way into nature. The minimal surface called a gyroid is topologically the boundary of a tubular neighborhood of the Laves graph, and this surface shows up in the structure of certain butterfly wings. For details, see:

• John Baez, The physics of butterfly wings, Azimuth, August 11, 2015.

• S. T. Hyde, M. O’Keeffe, and D. M. Proserpio, A short history of an elusive yet ubiquitous structure in chemistry, materials, and mathematics, Angew. Chem. Int. Ed. 47 (2008), 7996–8000.

Mathematically, the most interesting way to construct the Laves graph is as a ‘topological crystal’. This method was introduced by Sunada:

• Toshikazu Sunada, Crystals that nature might miss creating, Notices of the American Mathematical Society 55 (2008), 208–215.

• Toshikazu Sunada, Topological Crystallography, Springer, Berlin, 2012.

Just as the universal cover of a connected graph \(X\) has the fundamental group \(\pi_1(X)\) as its group of deck transformations, its maximal abelian cover, denoted \(\overline{X}\), has the abelianization of \(\pi_1(X)\) as its group of deck transformations. It thus covers every other connected cover of \(X\) whose group of deck transformations is abelian. Since the abelianization of \(\pi_1(X)\) is the first homology group \(H_1(X,\mathbb{Z})\), there is a close connection between the maximal abelian cover and homology theory.

For a large class of graphs there is a systematic way to embed the maximal abelian cover in the vector space \(H_1(X,\mathbb{R})\), the first homology group with real coefficients. We call this embedded copy of \(\overline{X}\) a ‘topological crystal’. When \(X\) is the complete graph with 4 vertices, \(H_1(X,\mathbb{R})\) is 3-dimensional Euclidean space, and the topological crystal is the Laves graph!

In more detail, the construction of topological crystals proceeds as follows. Any graph \(X\) has a space \(C_0(X,\mathbb{R})\) of 0-chains, which are formal linear combinations of vertices, and a space \(C_1(X,\mathbb{R})\) of 1-chains, which are formal linear combinations of edges. There is a boundary operator

$$ \partial \colon C_1(X,\mathbb{R}) \to C_0(X,\mathbb{R}) , $$

the linear operator sending any edge to the formal difference of its two endpoints. The kernel of this operator is the space of 1-cycles, \(Z_1(X,\mathbb{R})\). There is an inner product on the space of 1-chains such that edges form an orthonormal basis. This determines an orthogonal projection

$$ \pi \colon C_1(X,\mathbb{R}) \to Z_1(X,\mathbb{R}) . $$

For a graph we have \(H_1(X,\mathbb{R}) \cong Z_1(X,\mathbb{R})\). Thus, to build the topological crystal of \(X\), we only need to embed its maximal abelian cover \(\overline{X}\) in \(Z_1(X,\mathbb{R})\). We do this by embedding \(\overline{X}\) in \(C_1(X,\mathbb{R})\) and then projecting it down via \(\pi\).

To accomplish this, we need to fix a basepoint for \(X\). Each path \(\gamma\) in \(X\) starting at this basepoint determines a 1-chain \(c_\gamma\). It is easy to show that these 1-chains correspond to the vertices of \(\overline{X}\). Furthermore, the graph \(\overline{X}\) has an edge from \(c_\gamma\) to \(c_{\gamma’}\) whenever the path \(\gamma’\) is obtained by adding an extra edge to \(\gamma\). We can think of this edge as a straight line segment from \(c_\gamma\) to \(c_{\gamma’}\).

The hard part is checking that the projection \(\pi\) maps this copy of \(\overline{X}\) into \(Z_1(X,\mathbb{R})\) in a one-to-one manner. This happens precisely when the graph \(X\) has no bridges that is, edges whose removal would disconnect \(X\). The resulting copy of \(\overline{X}\) embedded in \(Z_1(X,\mathbb{R})\) is called a topological crystal.

For details, see:

• John Baez, Topological crystals.

This paper arose from a long discussion here:

• John Baez, Diamonds and triamonds, Azimuth, April 11, 2016.

The image of the unit cell of sphalerite was created by Benjah-bmm27 and put into the public domain on Wikicommons.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!