Diamond Cubic – Greg Egan

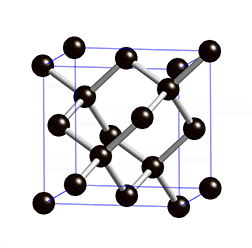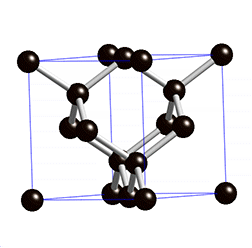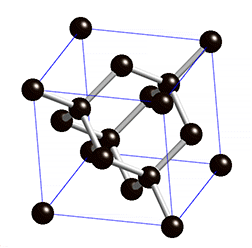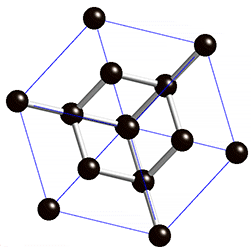
This picture by Greg Egan shows the pattern of carbon atoms in a diamond, called the ‘diamond cubic’. Each atom is bonded to four neighbors. This pattern is found not just in carbon but also other elements in the same column of the periodic table: silicon, germanium, and tin.

To build the diamond cubic, start with a cubical lattice, with an atom at each corner of each cube. Then put an atom in the center of each face of each cube. If we stopped there, we would have a face-centered cubic. But the face-centered cubic has points lying at the vertices of 4 tetrahedra in each cube, and if we add a point at the center of each tetrahedron, we obtain the diamond cubic:

Diamond Cubic – H. K. D. H. Bhadeshia

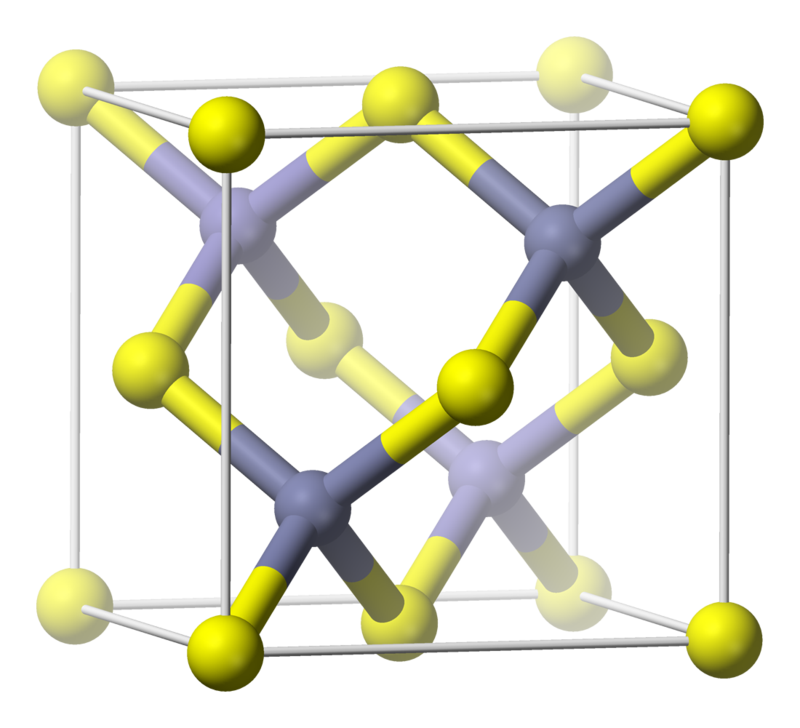
The mineral sphalerite, a form of zinc sulfide, crystallizes in the same pattern, but with alternating zinc and lead atoms. This picture clearly shows the four tetrahedra in each unit cell of the diamond cubic:

Sphalerite Unit Cell

In fact, the diamond cubic consists of two interpenetrating face-centered cubic lattices, with the second offset relative to the first along the main diagonal of the cubes in the first cubic lattice.

The face-centered cubic is the 3-dimensional version of a pattern that exists in any dimension: the \(\mathrm{D}_n\) lattice. To build this, take an n-dimensional checkerboard and alternately color the hypercubes red and black. Then, put a point in the center of each black hypercube. Equivalently, the \(\mathrm{D}_n\) lattice consists of all \(n\)-tuples of integers that sum to an even integer. Requiring that they sum to an even integer is a way to pick out the black hypercubes.

The diamond is also an example of a pattern that exists in any dimension. This is called \(\mathrm{D}^+_n\), because it is the union of two copies of the D_n lattice. To build it, first take all \(n\)-tuples of integers that sum to an even integer. Then take all those points shifted by the vector \((1/2, …, 1/2)\).

In any dimension, the volume of the unit cell of \(\mathrm{D}^+_n\) is 1, so we say it is unimodular. But only in even dimensions is the sum or difference of any two points in \(\mathrm{D}^+_n\) again a point in this set. In this case \(\mathrm{D}^+_n\) is a lattice: a discrete subgroup of \(\mathbb{R}^n\), whose vectors suffice to span \(\mathbb{R}^n\).

In dimensions that are multiples of 4, the \(\mathrm{D}^+_n\) lattice is better still: it is an integral lattice, meaning that the inner product of any two vectors in the lattice is again an integer.

In dimensions that are multiples of 8, the \(\mathrm{D}^+_n\) lattice is even better! It is an even lattice, meaning that the inner product of any vector with itself is even.

In fact, even unimodular lattices only exist in \(\mathbb{R}^n\) when \(n\) is a multiple of 8. In 8 dimensions, the only even unimodular lattice is \(\mathrm{D}^+_8\), which is usually called the \(\mathrm{E}_8\) lattice.

Returning to 3 dimensions, here is a very explicit description of the diamond cubic. It will be convenient to double the size of the diamond, so we can work with points all of whose coordinates are integers. So, start with a face-centered cubic consisting of points whose coordinates are even integers summing to a multiple of 4. It consists of these points:

$$ (0,0,0), \quad (2,2,0), \quad (2,0,2), \quad (0,2,2) $$

and all points obtained from these by adding multiples of 4 to any of the coordinates. To get the diamond cubic, we take this face-centered cubic together with another face-centered cubic that has been translated by the vector \((1,1,1)\). That consists of these points:

$$ (1,1,1), \quad (3,3,1), \quad (3,1,3), \quad (1,3,3) $$

and all points obtained by adding multiples of 4 to any of the coordinates.

For more on the diamond cubic, see:

• Diamond cubic, Wikipedia.

The diamond cubic can also be described as a ‘topological crystal’, as explained here:

• Toshikazu Sunada, Lecture on topological crystallography.

• Toshikazu Sunada, Topological Crystallography, Springer, Berlin, 2012.

• John Baez, Topological crystals.

The animated image of the diamond cubic was created by H. K. D. H. Bhadeshia and put into the public domain on Wikicommons.

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!