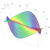
This is the {7,3,3} honeycomb as drawn by Danny Calegari using his program ‘kleinian’. In this image, hyperbolic space has been compressed down to an open ball using the so-called Poincaré ball model. The {7,3,3} honeycomb is built of regular heptagons in hyperbolic space. These heptagons lie on infinite sheets, each of which is a {7,3} tiling of the hyperbolic plane. The 3-dimensional regions bounded by these sheets are unbounded: they go off to infinity. They show up as holes here.

See also our article:

• {7,3} tiling.

Three sheets meet along each edge of the {7,3,3} honeycomb: this explains the final ‘3’ in the Schläfli symbol ‘{7,3,3}’. Four edges meet at each vertex, in a pattern with tetrahedral symmetry. Thus, six heptagons meet at each vertex. All this is a bit easier to see in the following picture of the closely related {6,3,3} honeycomb, which has hexagons instead of heptagons:

• {6,3,3} honeycomb.

The topology of the {7,3,3} honeycomb is interesting. It is simply connected, since all the holes extend all the way to the edge of Poincaré ball. Its ‘boundary’, that is, the set of points on the surface of the Poincaré ball that are limits of points in the {7,3,3} honeycomb, is homeomorphic to the Sierpinski carpet. See also:

• Sierpinski carpet.

The symmetry group of the {7,3,3} honeycomb is the Coxeter group

 

In other words, this group is generated by four reflections of hyperbolic 3-space, $s_1, \dots, s_4,$ obeying relations encoded in the edges of the diagram:

$$ (s_1 s_2)^7 = 1 $$
$$ (s_2 s_3)^3 = 1 $$
$$ (s_3 s_4)^3 = 1 $$

together with relations saying that each generator squares to 1 and distant ones commute:

$$ s_i s_j = s_j s_i \; \textrm{ if } \; |i – j| > 1 $$

More generally, any Coxeter group of the form

 

where $n \ge 7$ acts as symmetries of an {$n$,3,3} honeycomb. This honeycomb is a simply-connected 2-dimensional complex in hyperbolic 3-space whose faces are totally geodesic regular hyperbolic $n$-gons.

For an introduction to the software used to create this image, see:

• Danny Calegari, kleinian, a tool for visualizing Kleinian groups, Geometry and the Imagination, 4 March 2014.

Roice Nelson created another image of the {7,3,3} honeycomb:

Here each heptagon is subdivided into 7 red and 7 blue triangles. The {7,3,3} Coxeter group acts acts in a free and transitive way on these triangles, so if we choose a ‘favorite’ triangle, the set of these triangles can be identified with the Coxeter group itself. Nelson has also made a 3-dimensional model of the {7,3,3} honeycomb, available for sale at cost.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!