{7,3} Tiling – Anton Sherwood

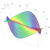
This is the {7,3} tiling: a tiling of the hyperbolic plane by equal-sized regular heptagons, 3 meeting at each vertex. The symmetry group of this tiling is the Coxeter group

which is generated by 3 reflections of the hyperbolic plane $s_1, s_2, s_3,$ obeying relations encoded in the edges of the diagram:

$$(s_1 s_2)^7 = 1$$
$$(s_2 s_3)^3 = 1$$

together with relations saying that each generator squares to 1 and distant ones commute:

$$s_1 s_3 = s_3 s_1$$

This group, also known as the (2,3,7) triangle group or $\Delta(2,3,7)$, is connected to a lot of interesting mathematics:

• (2,3,7) triangle group, Wikipedia.

For example, Klein’s quartic curve, the maximally symmetric 3-holed Riemann surface, can be tiled by 24 regular heptagons. The best way to see this is to describe Klein’s quartic curve as a quotient of the hyperbolic plane by a discrete group of symmetries that preserves the {7,3,3} tiling:

• John Baez, Klein’s quartic curve.

The image above is one among many generated by Anton Sherwood using a Python program. He put it in the public domain, and it is available on Wikicommons.

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!