The Ubiquity of Pi Day: It’s Not Just for Math Geeks

More and more every year, popular culture seems to be fascinated with Pi Day: the one day of the year where the infamous irrational number \( \pi = 3.14 \) is celebrated to eponymous accuracy, that is, on March 14. (In Europe the day in question is 14/03, but I’m assuming that a weblog for the American Mathematical Society will be mostly read by a North American audience.)

But why celebrate Pi Day? And how can we as educators use this as a learning moment in the classroom? I’d like to present ways you can discuss \( \pi \) in Religious Studies, Sociology, Computer Science, Mathematics, and Political Science. (Most of the post below comes from my web page here.)

Religious Studies: \( \pi \) in the Bible

The number \(\pi\) is defined as the ratio of the circumference of a circle to its diameter. This number has been around much much longer than one might expect. I was amazed to find that the Old Testament of the Bible even discusses the number \(\pi\)! For example, I Kings 7:23 reads: “[King Solomon] made the Sea of cast metal, circular in shape, measuring ten cubits from rim to rim and five cubits high. It took a line of thirty cubits to measure around it.”

Solomon’s Molten Sea

Since a cubit is about 1.50 feet (about 0.46 meters), it’s easy to see that \(\pi\) is approximately 3. Here are some questions one might wish to ask for discussion in the classroom.

• Does the Bible really say that \( \pi = 3 \)? Could the Bible be wrong about this?
• Are there other places in the Bible that mention \( \pi \)?
• Are there other well-known mathematical constants which appear in the Bible? That about other religious texts, such as the Quran or the Torah?

Sociology: \( \pi \) Across Cultures

The African engineer Archimedes of Syracuse (287 BC – 212 BC) found an even better approximation of \(\pi\) via his “method of exhaustion”: by comparing the circumference of the circle with the perimeters of the inscribed and circumscribed 96-sided regular polygons, he found \(\pi\) is somewhere between 223/71 = 3.14085 and 22/7 = 3.14286. The Chinese astronomer Zu Chongzhi (429 – 501 A.D.) realized \(22/7 = 3.14286\) approximates \(\pi\) to 2 decimal places, whereas \(355/113 = 3.14159\) approximates \(\pi\) to 6 decimal places. (The fractions are known in Chinese as Yuelu and Milu, respectively.)

• Why are \( 22/7 \) and \( 355/113 \) really good approximations to \( \pi \)? Are there other approximations which work even better?
• Does \( \pi \) or relatively good approximations have corresponding names in other cultures?

Computer Science: What Are The Digits of \( \pi \)?

With the introduction of calculus, one can compute \(\pi\) to as many digits as desired. The German mathematician Gottfried Wilhelm Leibniz (1646 – 1716), Scottish astronomer James Gregory (November 1638 – October 1675), and Indian astronomer Madhava of Sangamagrama (c. 1350 – 1425) each discovered the series expansion \( \displaystyle \sum_{k=0}^{\infty} (-1)^k \, \dfrac {1}{2k+1} = \dfrac {\pi}{4}\). Of course, this follows from the Maclaurin series expansion \(\arctan(x) = \displaystyle \sum_{k=0}^{\infty} (-1)^k \, \dfrac {x^{2k+1}}{2k+1} \) where one substitutes \(x = 1\). An even better approximation comes from setting \(x = \dfrac {1}{\sqrt{3}} \): \[ \pi = 6 \, \arctan \dfrac {1}{\sqrt{3}} = \sum_{k=0}^{\infty} \dfrac {(-1)^k}{2k+1} \, \dfrac {2 \, \sqrt{3}}{3^n} = 3.141592653589793 \dots. \]

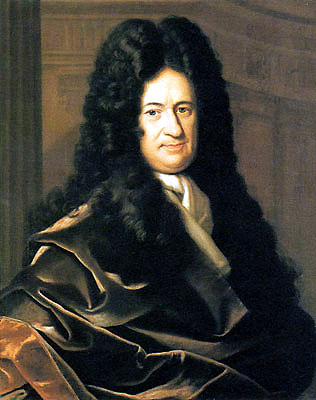
Gottfried Wilhelm Leibniz (1646 – 1716) and James Gregory (November 1638 – October 1675)

• What is pi-philology?
• What is a Feynman Point?
• How many digits of \( \pi \) can you recite? If you’re looking to memorize lots and lots of these digits, there’s a neat song on YouTube by Andrew Huang.

Number Theory: Irrationality of \(\pi\)

But is \(\pi\) a rational number? Can we find integers \(p\) and \(q\) such that \(\pi = p/q\)? In 1768, the Swiss mathematician Johann Heinrich Lambert (1728 – 1777) showed that the answer is no: \(\pi\) is an irrational number.

The Hungarian mathematician Miklos Laczkovich (1948 — ) gave a simplified version of Lambert’s argument in 1997. The idea is to introduce Bessel functions, that is, certain series solutions to the second order differential equation \( x^2 \, y” + x \, y’ + (x^2 – n^2) \, y = 0\): \[ J_n(x) = \left( \dfrac {x}{2} \right)^n \left[ \sum_{k=0}^{\infty} \dfrac {(-1)^k}{k! \, (k+n)!} \left( \dfrac {x}{2} \right)^{2k} \right] \qquad \text{where} \qquad k! = \int_0^\infty t^k \, e^{-t} dt. \]

Laczkovich showed the ratio \( x \, J_{n+1}(2x) / J_n(2x) \) is never a rational number whenever \(x^2\) is a nonzero rational number. Since
\[ \left. \begin{aligned}
J_{+1/2}(x) & = \sqrt{ \dfrac {2}{\pi x}} \, \sin x \\[5pt]
J_{-1/2}(x) & = \sqrt{ \dfrac {2}{\pi x}} \, \cos x
\end{aligned} \right \} \qquad \implies \qquad
\dfrac {x \, J_{n+1}(2x)}{J_n(2x)} = x \, \tan 2x \]
we may conclude (1) if \(x\) is a nonzero rational number, then \(\tan(x)\) is irrational and (2) \(\pi^2\) is irrational.

Curiously, American mathematician Noam Elkies (1966 -) observed that one can use the latter fact to conclude there are infinitely many rational primes. Indeed, if there were finitely many, then the left-hand side of Euler’s identity \( \displaystyle \prod_{\text{$p$ prime}} \dfrac {1}{1 – p^{-2}} = \dfrac {\pi^2}{6} \) would be a finite product, and hence a rational number.

Johann Heinrich Lambert (1728 – 1777), Miklos Laczkovich (1948 — ), and Noam Elkies (1966 -)

• Lambert showed that \( \pi \) is irrational, while Laczkovich showed that \(\pi^2\) is irrational. It is true that \( \pi^n \) is irrational for every integer \( n \)?
• Laczkovich also showed that \(\tan(x)\) is irrational whenever \(x\) is a nonzero rational number. Using this, are there other numbers \( x \) you can show are irrational?

Analysis: Transcendentiality of \(\pi\)

More than a century after Lambert’s result, many began to wonder how “irrational” \(\pi\) really is. One question that arose was whether one can “square the circle”. That is, is it possible to construct a square, using only a finite number of steps with compass and straightedge, having the same area as a given circle? In 1667, James Gregory gave a proof (albeit incorrect) that this is not possible.

Allow me to put this into a larger context. A rational number \(x = p/q\) can be thought of as a root of a linear polynomial \(f(x) = q \, x – p\) having integer coefficients. More generally, a number \(x\) is said to be algebraic if it is the root of some polynomial \(f(x) = a_n \, x^n + \cdots + a_1 \, x + a_0\) having integer coefficients \(a_k\). Clearly, rational numbers are algebraic, and even some irrational numbers (such as \(i = \sqrt{-1}\)) are algebraic. In fact, numbers which can be constructed using a finite number of steps with a compass and straightedge are also algebraic; this is a fact shown in many advanced Abstract Algebra courses today. Numbers which are not algebraic are said to be transcendental. In 1768 – in the same paper where he proved the irrationality of \(\pi\) – Lambert conjectured that \(\pi\) is transcendental, and hence “squaring the circle” should be impossible.

In 1882, the German mathematician Ferdinand von Lindemann (1852 – 1939) showed \(\pi\) is indeed transcendental. This follows as a special case of the Hermite-Lindemann-Weierstrass theorem: \(e^x\) is never algebraic whenever \(x\) is a nonzero algebraic number. If \(\pi\) were algebraic, then \(x = \pi \, i\) would also be algebraic, contradicting the fact that \(e^x = -1\) is algebraic. Lindemann’s was the first definite proof that “squaring the circle” is indeed impossible.

Ferdinand von Lindemann (1852 – 1939)

• \(e^x\) is never algebraic whenever \(x\) is a nonzero algebraic number. What if \( x \) is transcendental? For example, is \( e^\pi \) also a transcendental number?
• Does this work for other transcendental numbers other than \( e \)? For example, is it true that “\( \pi^x\) is never algebraic whenever \(x\) is a nonzero algebraic number”?

Political Science: Indiana \(\pi\) Bill

While Lindemann’s result was celebrated by research mathematicians, it was not well-known to amateurs. In 1896, Indiana physician and amateur mathematician Edwin J. Goodwin believed he had discovered a way to square the circle. He had constructed a circle with circumference 32 and diameter 10, and inscribed a square having sides of length 7. As you can guess, there are several problems here: the ratio of the circumference to the diameter \( 32/10 \neq \pi \), and the square should have sides of length \( \sqrt{5^2 + 5^2} = \sqrt{50} = 7.07107\). It appears that Goodwin misunderstood the idea of “squaring the circle:” he thought it meant one should inscribe a square within the circle. (Which Archimedes had already done some 2,000 years before anyway.)

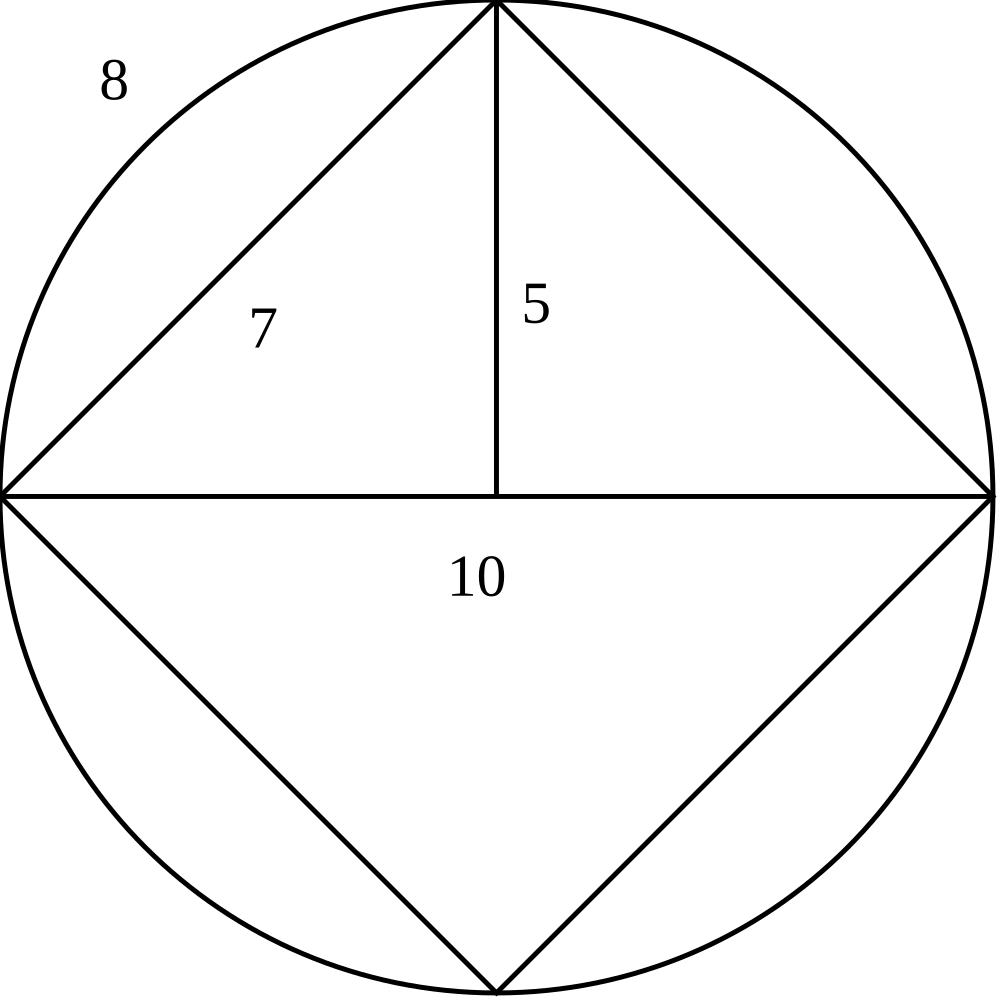
Goodwin’s Model Circle as Described in Section 2 of the Bill

Goodwin proposed a bill to his state representative Taylor I. Record stating that his result would appear free of charge in Indiana textbooks, and that the state would receive royalties for printing the result out of state. On January 18, 1897, Representative Record introduced the bill which read in part:

“[Goodwin’s] solutions of the trisection of the angle, doubling the cube and quadrature of the circle having been already accepted as contributions to science by the American Mathematical Monthly … And be it remembered that these noted problems had been long since given up by scientific bodies as unsolvable mysteries and above man’s ability to comprehend.”

The bill was introduced to the Indiana House of Representatives, but it caused a lot of confusion; Goodwin’s mathematics had claimed that the previous formulas involving the area for the circle were incorrect, although the bill itself was contradictory about the correct formula. On February 5, about the time the debate about the bill concluded, Purdue University professor Clarence Abiathar Waldo (1852 – 1926) arrived in Indianapolis to secure the annual appropriation for the Indiana Academy of Sciences. (Waldo was the president of the Academy that year.) An assemblyman handed him the bill, and Waldo pointed out the obvious mistakes, that is, that it is impossible to square the circle. (Recall that this had only been proved some 15 years before by Lindemann!) Still, the bill was tabled by the Indiana Senate, when one senator observed that the General Assembly lacked the power to define mathematical truth.

Clarence Abiathar Waldo (1852 – 1926)

You can read more about this history at Mental Floss. We in Indiana in general and Purdue in particular are grateful for Waldo’s intervention. If this fortunate series of events had not transpired, Hoosiers everywhere would be the laughing stock of the country for being those who legislated \( \pi = 3.2 \) as a rational number. Hopefully this will not be forgotten on this year’s Pi Day!