#Citations

Mathematicians are good at counting.  We can count the number of ways to roll  a 7 with two dice.  (Answer = 6.) We can count the number of ways to shuffle a deck of cards so that every card is not in its original position.  (Answer = $!52$ = 29672484407795138298279444403649511427278111361911893663894333196201.)  We can count the number of lines on a cubic surface in $mathbf{CP}^3$. (Answer = 27.)   Sometimes we can count, but we don’t really know what the actual number is, such as when we count the minimum number of guests that must be invited so that at least $m$ will know each other or at least $n$ will not know each other.  (Answer = the Ramsey number $R(m, n)$.)  Many times, it is better to use an asymptotic estimate, such as Stirling’s formula.  When we can’t estimate, we can bound, such as Conrey’s result that more than two-fifths of the zeros of the Riemann zeta function are on the critical line.  Lately, we (along with our colleagues in other disciplines) have started counting citations.  

What could go wrong?

Plenty.  Citation counts depend on matching algorithms.  The algorithms try to pair an item in the reference list of an article with a known item in a database.  Usually, you want to have matches or near matches on multiple points: author name, title, year of publication, page range, source (name of the journal).  However, bibliographic styles are not consistent.  And some authors make mistakes or take shortcuts, providing too little information.  Some journals enforce telegraphic reference styles.  Here is an example I chose at random from a respected physics journal:

• R. Yang and Z. Q. Wu, Earth Planet. Sci. Lett. 404, 14 (2014).
• J. C. Crowhurst, J. M. Brown, A. F. Goncharov, and S. D. Jacobsen, Science 319, 451 (2008).
• H. Marquardt, S. Speziale, H. J. Reichmann, D. J. Frost, and F. R. Schilling, Earth Planet. Sci. Lett. 287, 345 (2009).

Note that there are no titles.  Also, a page range isn’t given, just a starting page.  This style makes it hard for the matching algorithm, but it is a standard style in the physics literature, not just this journal.

Some old-school citations are almost impossible for an algorithm to find.  Here’s an old old-school example, from an old paper by Lefschetz in the Annals of Mathematics in 1920 .

   • • • • •

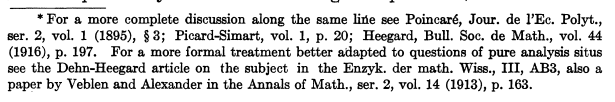
The references are given almost as prose, but heavily abbreviated.    My copy of Whittaker and Watson is  full of citations as footnotes.  (And I can only imagine how many times that book is referenced the way I just did, by the authors’ names, not by the title.¹)    Such citations are rarer now, but they still occur.

Errors in citations can propagate.  When I wrote my PhD thesis, an important result that I used was the Borel-Weil-Bott Theorem.  Bott’s paper is

MR0089473
Bott, Raoul
Homogeneous vector bundles.
Ann. of Math. (2) 66 (1957), 203–248.

However, I found that many papers cited it incorrectly.  Moreover, I could see that some authors copied the citation to Bott’s paper from the references in another paper.  If one paper had it incorrect, then subsequent articles make the same mistake.  I don’t remember exactly which ones I encountered way back in grad school, but examples are easy to find.  For instance, one paper has the year and pages correct, but has the volume number as 56.  Another puts the volume number at 60.  (Getting warmer!)  Kostant’s paper establishing his famous formula for the multiplicity of a weight gets everything right except the page range.  In his paper on Lie algebra cohomology and the Borel-Weil-Bott Theorem (published two years later), Kostant has a complete and correct citation.

Special Case: Books

Citations to books can be troublesome.   Often, the citation is spare, giving the author, title, and year.  Here is a citation from a paper published in 2016 to a famous book by Dautray and Lions:

21. Dautray R, Lions JL. Mathematical Analysis and Numerical Methods for Sciences and Technology. Springer: Berlin, 1990.

We matched that to

MR1036731
Dautray, Robert(F-POLY); Lions, Jacques-Louis(F-CDF)
Mathematical analysis and numerical methods for science and technology. Vol. 1.
Physical origins and classical methods. With the collaboration of Philippe Bénilan, Michel Cessenat, André Gervat, Alain Kavenoky and Hélène Lanchon. Translated from the French by Ian N. Sneddon. With a preface by Jean Teillac. Springer-Verlag, Berlin, 1990. xviii+695 pp. ISBN: 3-540-50207-6; 3-540-66097-6.

But it could also have been Volume 3 or Volume 4, which were also published in 1990:

MR1064315
Dautray, Robert(F-POLY); Lions, Jacques-Louis(F-CDF)
Mathematical analysis and numerical methods for science and technology. Vol. 3.
Spectral theory and applications. With the collaboration of Michel Artola and Michel Cessenat. Translated from the French by John C. Amson. Springer-Verlag, Berlin, 1990. x+515 pp. ISBN: 3-540-50208-4; 3-540-66099-2

MR1081946
Dautray, Robert(F-POLY); Lions, Jacques-Louis(F-CDF)
Mathematical analysis and numerical methods for science and technology. Vol. 4.
Integral equations and numerical methods. With the collaboration of Michel Artola, Philippe Bénilan, Michel Bernadou, Michel Cessenat, Jean-Claude Nédélec, Jacques Planchard and Bruno Scheurer. Translated from the French by John C. Amson. Springer-Verlag, Berlin, 1990. x+465 pp. ISBN: 3-540-50209-2; 3-540-66100-X

Volume 2 was published in 1988.  Volume 5 was 1992, and Volume 6 was 1993.

Formats vary greatly, with some including the city of publication, some including series information (such as Ergebnisse or maybe Ergebnisse der Mathematik or Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge).  If the series information is given, a volume number might be included.   In checking changes in citations after releasing the new  features for MathSciNet, we realized that there were instances of a citation to a book in a series mixing up the volume number and the year of publication.  (We fixed them.)

What can go right?

The propagation of the errors with citations to Bott’s paper described above was partly due to authors taking a shortcut.  Few people wanted to figure out the appropriate abbreviation for the Annals of Mathematics or where to put the volume number versus the publication year.  So many of us looked at the references in another paper to sort that out. With some of the tools built into MathSciNet, such shortcuts are no longer necessary.  At Mathematical Reviews, we work very hard to make sure we have complete and accurate bibliographic information for the entries in MathSciNet.  We also work hard to make it easy for you to use that information.  My earlier post References and Citations tells you ways to do that, including obtaining the information in BibTeX format.

If you use the bibliographic data from MathSciNet in your references, then everybody’s matching algorithms will have a much easier time pairing those references with the paper in their databases.  This helps people count.  And you will have an easier time writing up the paper!

¹ This is related to the problem of Alice’s Restaurant.  Sometimes what we call a thing is not the name of the thing. There is a song called Alice’s Restaurant, which is about Alice’s restaurant.  But “Alice’s Restaurant” is not the name of the restaurant – it’s just the name of the song about the restaurant.