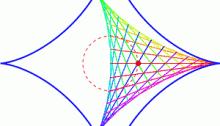
Romik’s Ambidextrous Sofa
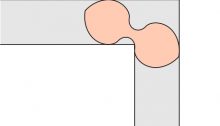
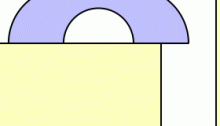
The ambidextrous moving sofa problem is to find the planar shape of maximal area that can negotiate right-angled turns both to the right and to the left in a hallway of width 1. The current best known solution was found by Dan Romik, and is shown here.